Matheminecraft

Illustration Promotion des maths EPFL 2020
Faire des maths en jouant à un jeu vidéo ? Si, si, c’est possible avec matheminecraft ! Découvre cette carte aventure un peu spéciale, créé par l’équipe de promotion des maths de l’EPFL !
Activité 1
Pour faire cette 1ère activité, il te faudra :
- Du papier
- Un crayon
Pour commencer, essaie de trouver des dessins fermés qui se font sans lever le crayon.
Alors, en as-tu trouvé ?
En voici quelques exemples :
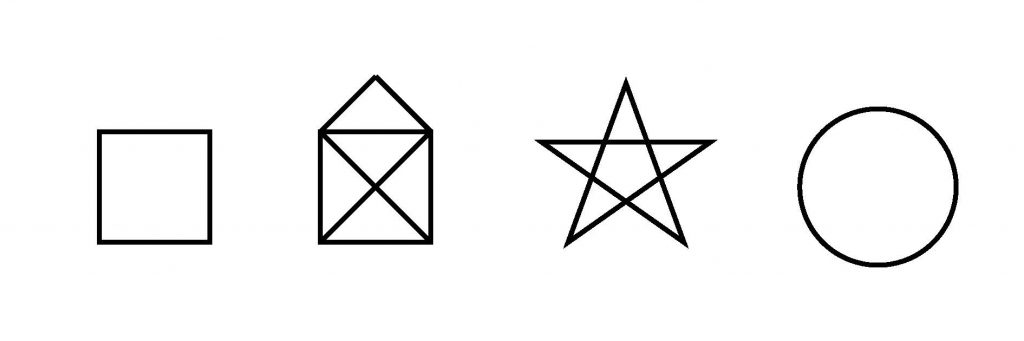
Il s’agit de cycles eulériens, c’est-à-dire qu’on arrive à les dessiner et à revenir au point de départ, sans lever le crayon.
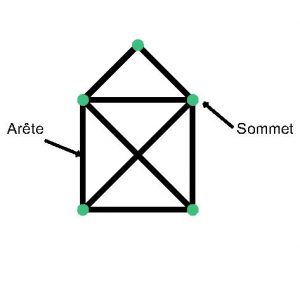
En mathématiques, les traits sont appelés des arêtes et les coins des sommets.
Maintenant que tu as découvert ces quelques exemples de cycles eulériens, essaye de résoudre le même problème qu’Euler !
En effet, le mathématicien suisse Léonhard Euler est le premier à s’être intéressé à la question. Il a de ce fait fondé la théorie des graphes.
Un des premiers problèmes résolus par Euler est le suivant : la ville de Königsberg est constituée de 2 îles, reliées par un pont. Il existe également 6 autres ponts, comme dessiné sur la carte ci-dessous. Existe-t-il une promenade dans la ville de Königsberg qui passe par les 7 ponts, et chacun une seule fois ?
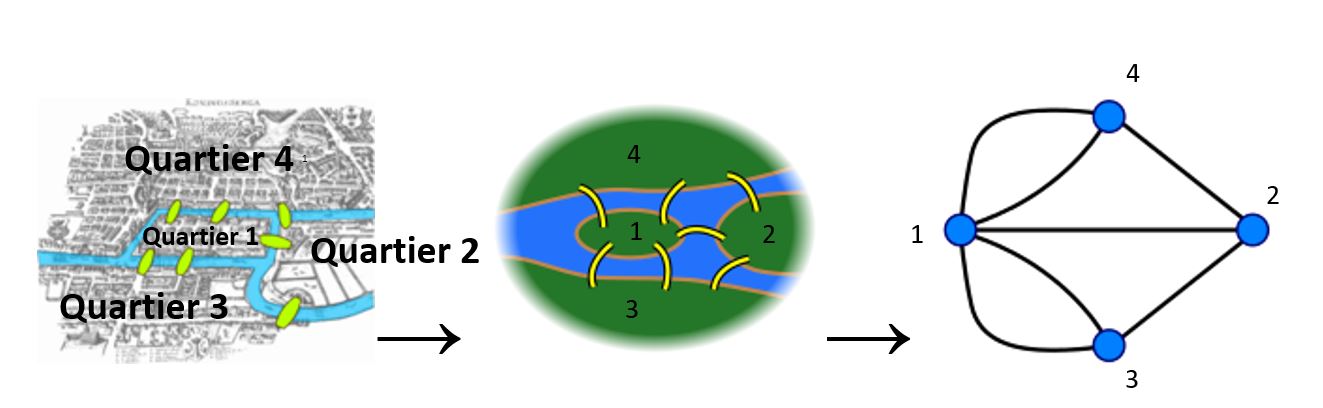
Alors as-tu résolu le problème ?
Vérifie ton raisonnement avec les explications ci-dessous :
Tu n’as pas trouvé de solution et bien tu as raison !
Euler fut le premier à déterminer qu’il n’existe pas de solution à ce problème.
En effet, le théorème énoncé par Euler dit qu’un graphe admet un cycle eulérien si et seulement si, de chacun de ses sommets, sort un nombre pair d’arêtes (on dit que le degré des sommets est pair). Dans ce cas, on peut parcourir le graphe en ne passant qu’une fois sur chaque arête, et revenir au point de départ.
Exemple de graphe admettant un cycle eulérien :
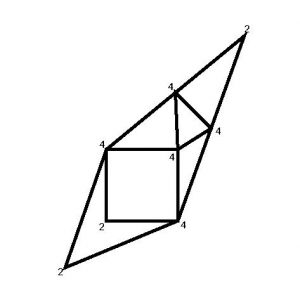
Et un graphe admet une chaine eulérienne (un chemin qui passe par chaque arête une seule fois mais ne revient pas forcément au point de départ) si :
- tous les sommets sont de degré pair : cas du cycle eulérien vu dans le paragraphe ci-dessus.
- ou si exactement deux sommets sont de degré impair. Il est alors possible de parcourir le graphe en ne passant qu’une fois sur chaque arête, mais sans revenir au point de départ.
Exemple : enveloppe ouverte
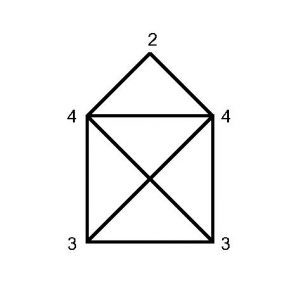
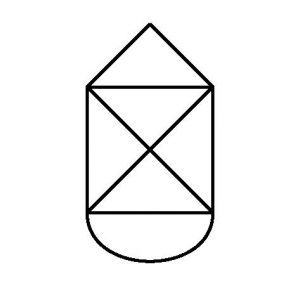
Si on ajoute une arête qui relie les 2 sommets dont le degré est impair, on obtient une chaine eulérienne fermée et le graphe devient donc un cycle eulérien. On peut de nouveau le parcourir en ne passant qu’une fois sur chaque arête et revenir au point de départ.
Exemple :
Applications
La théorie des graphes est une branche des mathématiques comme la géométrie ou la logique. C’est un outil très utilisé dans de nombreux domaines. Planifier des routes efficaces pour distribuer le courrier ou ramasser les ordures, effectuer des diagnostics dans les réseaux informatiques, planifier les voies aériennes entre des aéroports, gérer un réseau électrique, etc. sont autant d’exemples concrets utilisant cette théorie.
La théorie des graphes est très vaste et de nombreux autres problèmes existent: comment passer par tous les sommets d’un graphe ? Quel est le plus court chemin passant par tous les sommets d’un graphe et revenant au point de départ (problème du voyageur de commerce) ? Etc.
Une partie des recherches en théorie des graphes consiste à trouver les algorithmes qui permettent de résoudre ces problèmes.
Activité 2
Pour faire cette 2e activité, il te faudra :
- Un ordinateur
- Le jeu minecraft (attention, il est payant) et l’extension matheminecraft que tu peux télécharger ici .
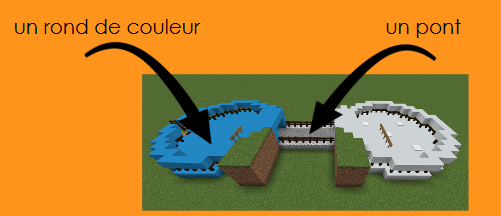
Dans le jeu matheminecraft, c’est le même principe que les dessins que l’on a faits dans la première activité! Les graphes sont déjà dessinés, et c’est à toi de trouver le chemin qui te permet de les parcourir, sans passer 2 fois sur la même arête. A toi donc de déterminer le cycle eulérien admis par ces graphes !
Les arêtes sont représentées par des ponts, et les sommets par des ronds de couleurs.
Photographie, toi aussi, tes dessins et partage nous ton résultat sur les réseaux sociaux :
@EPFL_SPS
Si tu n’as pas accès à ces réseaux sociaux, tu peux toujours nous envoyer ta vidéo par mail, elle sera peut-être publiée sur nos réseaux !

Page d’accueil : Les sciences à la maison
Durant la période d’arrêt de fréquentation des lieux de formation, le Service de promotion des sciences de l’EPFL propose aux curieuses et curieux de tout âge, des activités scientifiques et techniques à faire à la maison.


