Propriétés des parallélogrammes
Ce film d’une dizaine de minutes concerne le Corollaire 3.4 dont vous recopierez la preuve à la page 31, et les caractérisations de la Proposition 3.5. Je prouve la première qui est un exercice de la Série 29, profitez donc de la recopier sur la page de gauche, surtout si vous n’avez pas gardé une copie propre de l’exercice fait en classe!
Les rectangles
Dans cette vidéo de 10 minutes nous définissons les rectangles et montrons la Proposition 4.2 à écrire à la page 32.
Les rhomboïdes
Ce film de 7 minutes concerne les rhomboïdes, les losanges et les carrés. En gros il vous suffira de compléter le dessin de la page 33 et de faire les dessins de la page 34 pour illustrer les propriétés des losanges et des carrés.
Polygones réguliers
Pour terminer ce Chapitre 3 on parle encore rapidement (4 minutes) des polygones réguliers. Copiez les calculs d’angles au bas de la page 35. Les calculs sont corrects mais il y a un moment où je dis que l’angle gamma mesure 180 degrés, ce qui est faux (c’est 108).
Position relative de deux cercles
Nous commençons maintenant le Chapitre 4 avec un film de 9 minutes sur les pages 36 et 37 du fascicule. Les définitions et résultats préparent la suite sur les positions relatives de deux cercles.
Cercles sécants ou tangents?
On démontre en moins de 7 minutes les deux critères qui nous permettent de reconnaître des cercles sécants ou tangents en fonction des rayons et de la distance entre les centres de ces cercles. Ceci vous aidera à compléter les pages 37, 38 et 39.
Un cercle et une droite
Cet autre film de 7 minutes utilise les résultats de la vidéo précédente pour comprendre les différentes positions relatives entre un cercle et une droite. Il vous permet de compléter le cours aux pages 40, 41 et 42.
Serie30 du 5 mai
Exercice 1. En joignant les milieux des côtés d’un quadrilatère convexe, on forme un nouveau quadrilatère. Pour illustrer cela, regardons le cas du rectangle. Nous devons construire les milieux E, F, G et H de chacun des côtés du rectangle et les relier entre eux, comme sur la figure suivante:
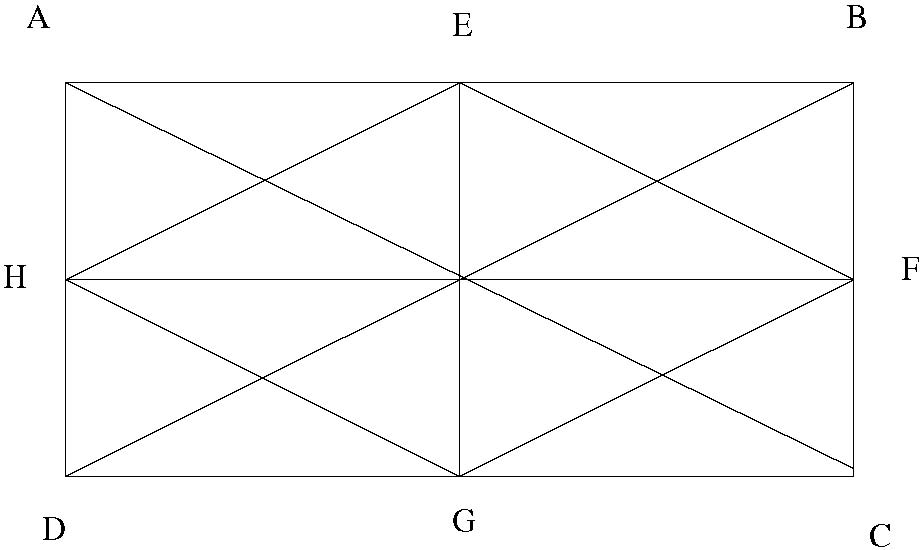
Le quadrilatère EFGH est un … losange! Pourquoi? Relis la définition d’un losange et explique pourquoi les diagonales de EFGH sont des axes de symétrie de ce quadrilatère.
Exercice 5, partie 2 et 3. Pour comprendre où se trouve le centre du cercle circonscrit à un triangle ABC rectangle en A, je vous propose de construire le symétrique de ce triangle par rapport au milieu M de l’hypoténuse (il s’agit d’une symétrie centrale!). En observant attentivement cette figure vous devriez pouvoir montrer rapidement la partie 2. Pour la partie 3, utiliser la partie 2 pour montrer que le point M se trouve à égale distance des trois sommets A, B et C.
Exercice 8. Un élève a posé la question suivante: Pour le (a), j’ai trouvé seulement un quadrilatère, qui correspond au (b) (il a un centre de symétrie). Donc existe-t-il un quadrilatère qui a les propriétés du (a), mais pas de centre de symétrie ? Et pour le (b), doit-on justifier la réponse à la question “Est-il simple ?”
On pourrait effectivement dessiner deux fois le même quadrilatère, mais l’idée est d’en trouver deux différents! Je vous propose de réfléchir à la question « est-il simple? », à prendre comme une indication.(voir ci-dessous après si ce n’est pas assez clair). Pour la justification, comme je vous demande un exemple, il suffit de se baser sur l’observation de votre exemple.
Spoiler: L’une des caractérisations des parallélogrammes que nous avons vue en cours nous indique que si le quadrilatère est simple alors ce sera un parallélogramme. Ceci indique comment tracer deux côtés opposés isométriques. Il faudra probablement choisir un quadrilatère non simple!
Exercice 12. Souvent, pour résoudre un exercice, c’est une bonne idée de supposer que le problème est résolu. Pour un exercice de construction de figures géométriques, cela signifie qu’on va faire un croquis de la figure à construire (on suppose donc qu’on l’a déjà construite!). Les observations que l’on pourra faire sur ce croquis serviront alors à comprendre les propriétés de la figure et nous guideront ensuite vers la marche-à-suivre (à la règle et au compas). Je vous demande dans chaque cas de rédiger soigneuseument une marche-à-suivre, point par point, chaque point de la construction sur une ligne.
En particulier pour le (d), faites un croquis et si vous avez besoin d’une indication, essayez de dessiner sur votre croquis le symétrique du trapèze cherché par rapport au milieu d’un des côtés (pas les bases), ou tracez une parallèle à l’un de ces côtés qui passe par un autre sommet, bref ramenez-vous à la construction d’un parallélogramme, ce qui est plus facile!