Exercise worksheets with Jupyter notebooks
With their built-in interactivity, Jupyter Notebooks allow you to easily design a variety of exercises and problems that will provide students with unique opportunities to practice and apply what they have learned while developing their computational thinking skills.
Find out below how to:
- Build progression into your worksheets
- Teach problem solving strategies
- Provide students with feedback (automated or not)
- Make sure students learn what you want them to learn
- Embed multimedia activities into your worksheets
- Design content-writing tasks for your students
Discover the notebook-based exercise worksheets of Guillaume Anciaux in his civil engineering course
Four keys for effective exercise worksheets in notebooks
In this section, we draw on the literature on problem solving and computing education to provide you with four essential keys to design effective exercise worksheets with Jupyter notebooks.
Key #1: build progression into your worksheets
The literature on problem solving has shown that starting worksheets with simpler highly-guided exercises but progressively increasing the level complexity while gradually decreasing the amount of guidance improves students’ performance on complex problem solving. Called scaffolding, this approach is also effective with programming activities (Robins, 2019), where designing a program to solve a problem can be classified among the most complex tasks from a cognitive point of view. How to proceed in practice?
In practice, this means that when students learn to solve complex problems, they will highly benefit from introductory tasks such as recall quiz questions, worked examples and simpler or more structured problems. In the context of programming, starting your exercise worksheets with code reading activities, followed by activities with code to modify or to complete is therefore likely to be more effective than starting directly with activities requiring students to write code from scratch.
To engage students in reading code, you can ask them questions such as to predict the execution result or to sketch the execution trace with the state of the different variables over time. Fixing or correcting programs also make highly valuable activities to familiarize students with deciphering error messages as well as with testing and debugging, essential skills for computational scientists, engineers and programmers.
Key #2: teach problem solving strategies
Teaching a problem solving method to students is among the most effective instructional strategies (Hattie, 2009). This means that you can greatly help your students by guiding them to a structured approach to problems, emphasizing in particular how to analyze a problem and how to check their work (without using the solution). This can be achieved, for instance, by making those steps explicit in exercise questions and in solutions. But there are two other ways in which you can help students become better problem solvers.
A key underlying issue is that students will not necessarily learn problem solving strategies from programming solutions to problems. Among the many reasons for this effect is that it is very hard to learn from doing something (here, programming) because all the resources of our cognitive system are dedicated to the task. We actually learn from reflecting on what we do (Dewey, 1933). You can therefore help your students become better problem solvers and programmers by including reflection questions at the end of your exercises such as: “summarize the steps involved in designing a solution to an optimization problem based on gradient descent”. You can encourage them to take notes of their answer by including an empty raw cell into your notebook for instance.
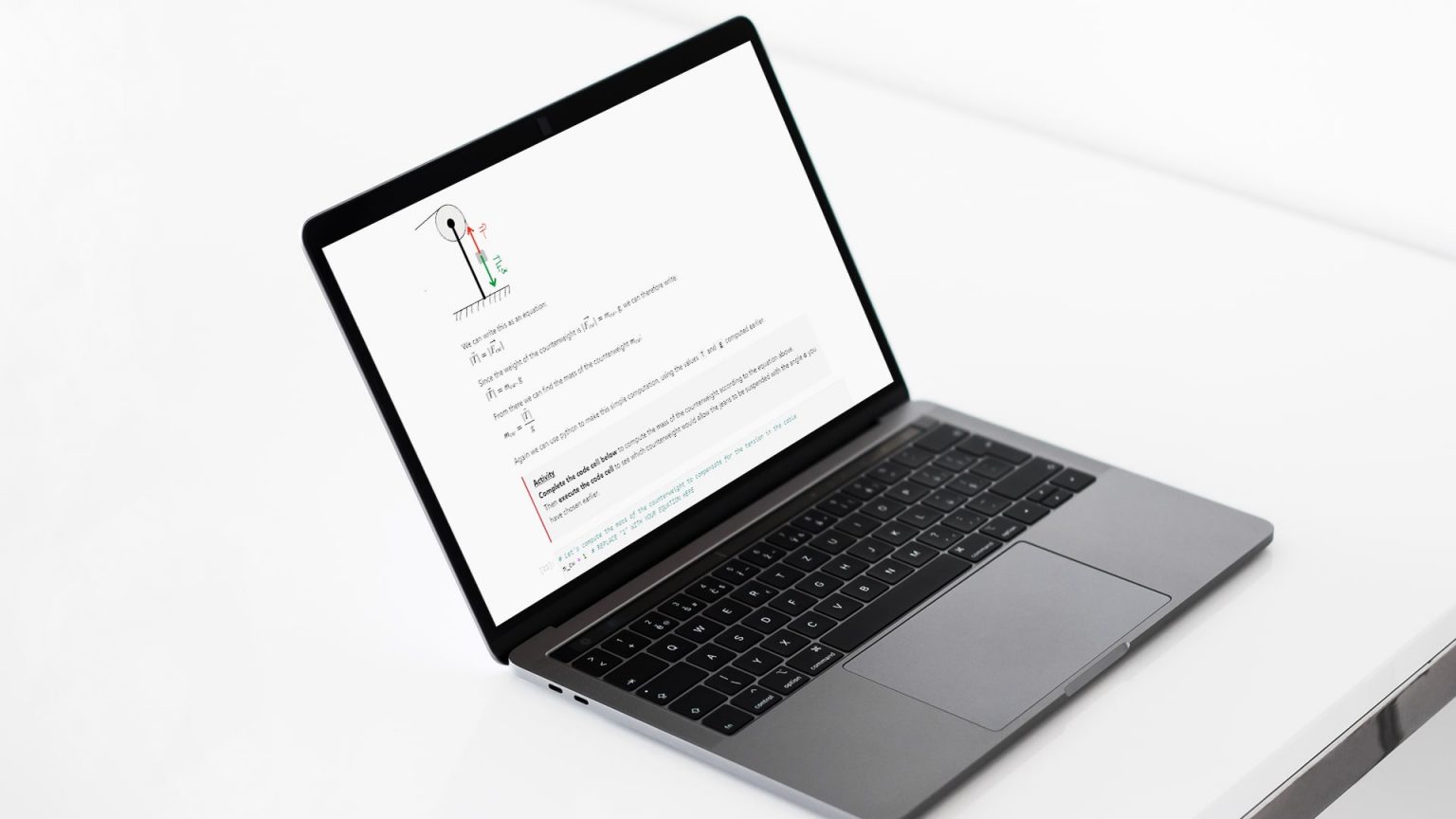
Leading students to think on paper rather than directly with the keyboard is another helpful teaching technique (Cunningham et al., 2017). Although notebooks are designed for exploratory problem solving, they cannot (yet) replace paper notebooks when it comes to sketching – a thinking tool of utmost importance in computation and more generally in science and engineering (Dym et al., 2005). Therefore, don’t hesitate to include questions that require students to work on paper in your notebook worksheets.
Key #3: provide students with feedback
Students often struggle to identify whether they solved a problem successfully or not. This lies, in part, in a lack of verification skills and habits. In programming, because there are so many ways to get to the same result, including wrong or poorly performing ones, testing abilities are key. Notebooks make it easy to provide students with ways to get feedback automatically on their solutions, while developing their testing skills. We detail three different ways of providing students with useful feedback below.
Taking advantage of the built-in execution feedback loop of notebooks, one simple option is to indicate to students specific inputs against which to run their program along with reference outputs they should compare to. In his image processing labs, Pol del Aguila Pla has implemented this solution in the form of systematic “sanity checks” that students can run to test their program – read his story here.
In that context, training students to identify and make their solutions robust to edge cases, i.e. extreme or particular values that can result in the failure of a system, is particularly important. And if your goals include teaching formal testing procedures to students, then you can provide them with sets of test cases based on Python assertions or unit test libraries for instance, with a progression towards students writing the tests themselves.
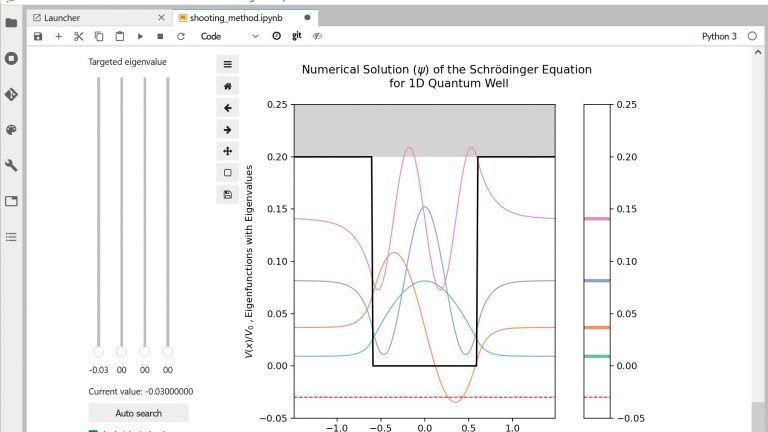
Providing students with a way to visualize graphically their results can also make feedback more concrete. A pre-written function generating a plot or a visualization taking their result as an input can be an effective way for students to see whether they are on the right track or not. For example, Guillaume Anciaux provides students with functions to display matrices and to plot corresponding mesh structures. Learn more with his story here.
Finally, solutions are also a way to provide students with valuable feedback, in particular when they model the type of expert thinking students should aim at. You can “hide” solutions into your notebooks using the built-in mechanism for collapsing cells: simply click on the blue bar on the left side of a selected cell – see the official documentation here. More detailed solutions can be provided in the form of complete notebooks, which often allows more space for guiding students in the type of thinking you expect them to develop.
Key #4: make learning goals and important information visible
One issue students have with exercises, particularly programming exercises, is to identify what they should retain from doing them. For instance, in a notebook about inferential statistics, should they memorize the exact R syntax for performing a two-sample t-test or should they recall the methodological steps of statistical hypothesis testing? We review two different ways in which you can help students learn from exercises in notebooks.
By making clear to students from the beginning of your notebook what they should learn and which skills you expect them to practice, you increase the chances that your students learn what you want them to learn from doing the exercises. For instance, in a notebook where students practice with SQL queries, a learning goal could be: “you should be able to explain the differences between the SQL set operations UNION, INTERSECT and EXCEPT”.
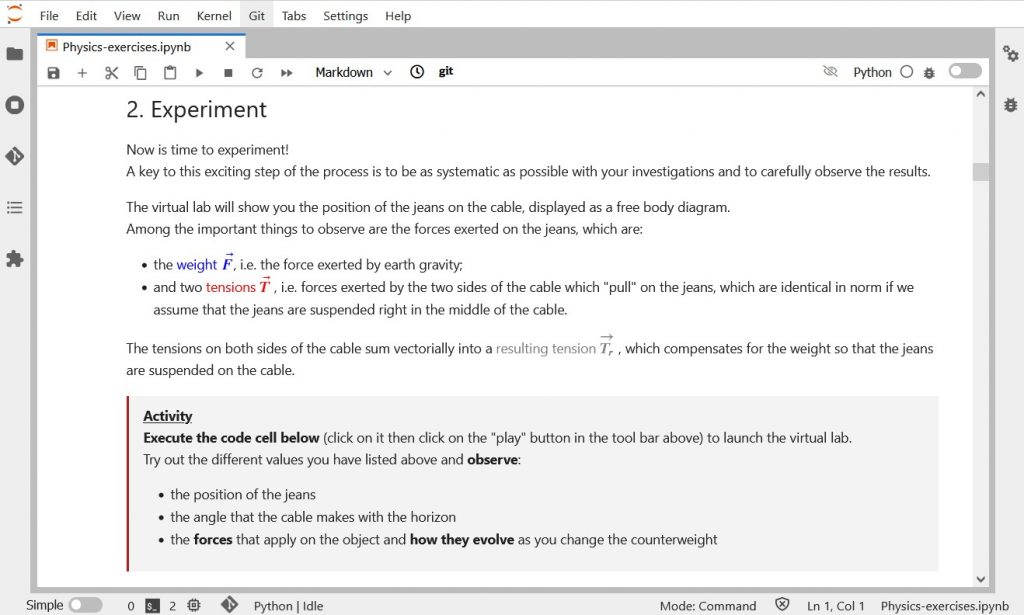
If your exercise worksheet contains explanatory text and examples (which is a good thing!), students might have difficulties to identify important information and determine what they are expected to do. Highlighting important information and making instructions clearly visible is part of a good notebook worksheet design. While the formatting options of Markdown are quite limited, the good news is that you can use HTML and CSS markup in markdown cells. As illustrated by the figure below, using <div> blocks with background and border coloring can help make relevant information more visible.
Wondering if your notebook is well designed? Self-assess your notebook using our rubric!
Multimedia activities in notebooks
Notebooks are so flexible that they can embed a range of multimedia activities. Auto-graded quizzes are among the easiest to implement and they make great warm-up activities at the start of your exercise worksheets. No need for you to write any piece of code, you can simply embed interactive H5P activities (supported by many learning management systems such as Moodle, Canvas or Blackboard), into a notebook using an HTML iFrame. For EPFL teachers, please check the documentation here. Alternatively, the Python library “jupyterquiz” by John M. Shea allows you to easily create multiple choice questions as well as numerical questions for your Jupyter notebooks.
Asking students to write content in notebooks
Asking students to write content in notebooks is also possible and a valuable type of activity as putting words on thoughts is generally helpful for understanding. As we have seen above, raw cells make simple note taking placeholders. But if you want students to engage in more elaborate writing, then you should consider introducing students to the bases of Markdown and eventually to LaTeX equations if necessary. Document edition and preparation skills are the kind of transversal skills useful to students independently from their discipline! We share with you some useful resources at the end of our page on using Jupyter notebooks in projects and labs.
Author: Cécile Hardebolle
Other resources
Discover other ways of using Jupyter Notebooks in your teaching
Bibliography
Cunningham, K., Blanchard, S., Ericson, B., & Guzdial, M. (2017). Using Tracing and Sketching to Solve Programming Problems: Replicating and Extending an Analysis of What Students Draw. Proceedings of the 2017 ACM Conference on International Computing Education Research – ICER ’17, 164–172. https://doi.org/10.1145/3105726.3106190
Dewey, J. (1933). How we think: A restatement of the relation of reflective thinking to the educative process. D.C. Heath.
Dym, C. L., Agogino, A. M., Eris, O., Frey, D. D., & Leifer, L. J. (2005). Engineering Design Thinking, Teaching, and Learning. Journal of Engineering Education, 94(1), 103–120. https://doi.org/10.1002/j.2168-9830.2005.tb00832.x
Hattie, J. (2009). Visible learning: A synthesis of over 800 meta-analyses relating to achievement. Routledge.
Robins, A. V. (2019). Novice Programmers and Introductory Programming. In The Cambridge Handbook of Computing Education Research (p. pp 327-376). Cambridge University Press. https://doi.org/10.1017/9781108654555.013