Fundamentals of Atomistic Machine Learning

A key goal of atomistic modeling is to find the relationship between a given structure and its properties. To find this relationship, we need to build a representation of the structure and a model that relates this representation to the target properties.

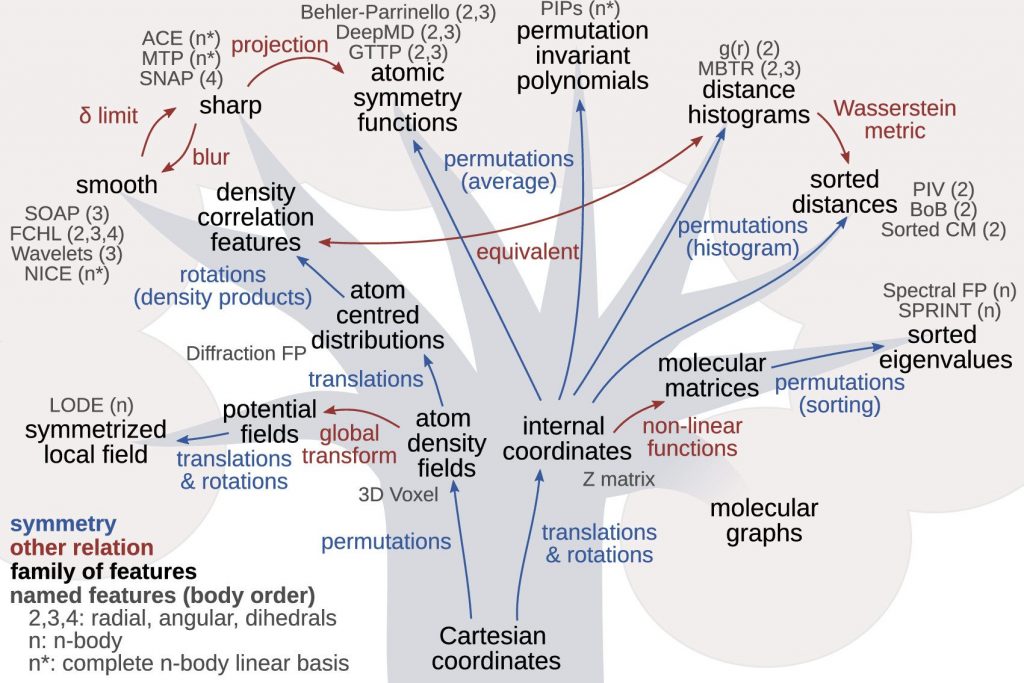
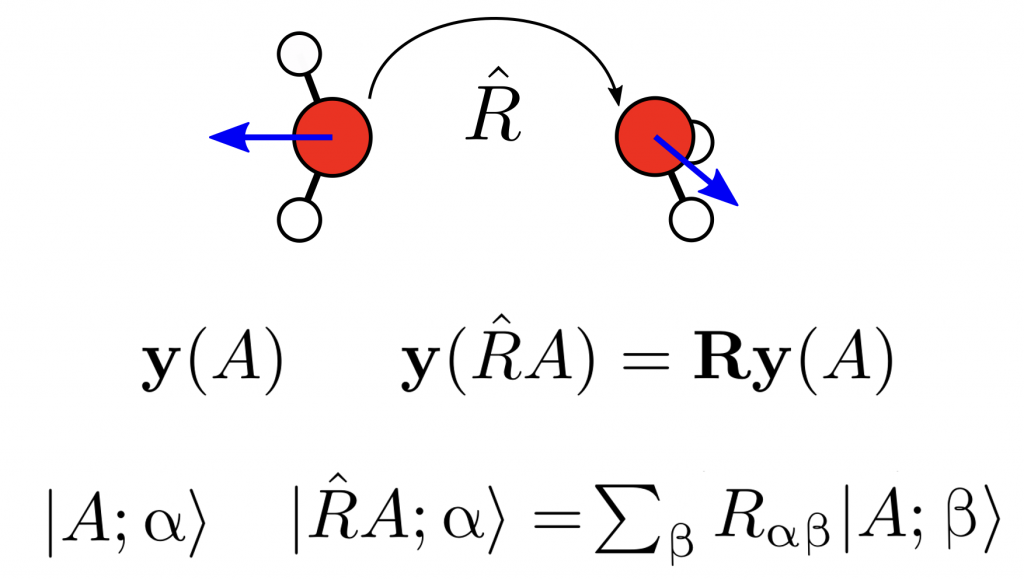
Phylogenetic tree of structural representations for materials and molecules. Arrows indicate the relationship between different groups of features. Lists of names, in gray, indicate the most common implementations for each class. Classes that appear as “leaves” of the tree are fully symmetric.

In our group, we investigate the fundamental questions related to the mathematical representations by studying their equivariance under basic physical symmetries, their smoothness and additivity. We also study solutions to the issue of the lack of completeness of some commonly employed representations, whereby two physically different atomic structures share the same representation. 

The transformations of a molecular vector property under the action of a rigid rotation. The descriptors also transform in a prescribed way to preserve equivariance.

Beyond that, we are putting our efforts into creating new models for more accurate predictions and estimating the uncertainty that should be ascribed to machine learning models. We also develop auxiliary techniques for analysing and reducing the complexity of big datasets, and to get a physical interpretation of the local quantities, like local energies or local dipoles, predicted via machine learning approaches.