Learning a convolutional filter bank on the CIFAR-10 dataset Sparse representations are at the heart of many modern Machine Learning algorithms. Particularly relevant to the Computer Vision community is the possibility to learn filter banks (also called dictionaries) tuned to the statistics of the data.
Learning a convolutional filter bank on the CIFAR-10 dataset Sparse representations are at the heart of many modern Machine Learning algorithms. Particularly relevant to the Computer Vision community is the possibility to learn filter banks (also called dictionaries) tuned to the statistics of the data.
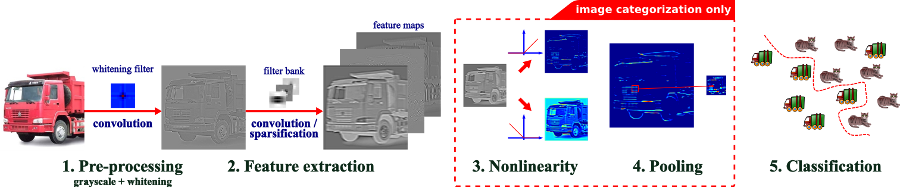
We have investigated a convolutional approach to learn, under sparsity constraints, a set of filters for image categorization and pixel classification purposes. We have then set up a shallow classification pipeline to evaluate whether these constraints play a role also at run-time.
We show that, while learned filters are able to outperform handcrafted approaches in both tasks, enforcing sparsity constraints on features extracted in a convolutional architecture does not improve classification performance.
This is very relevant for practical purposes, since it implies that the expensive run-time optimization required to sparsify the representation is not always justified, and therefore the computational costs can be drastically reduced.
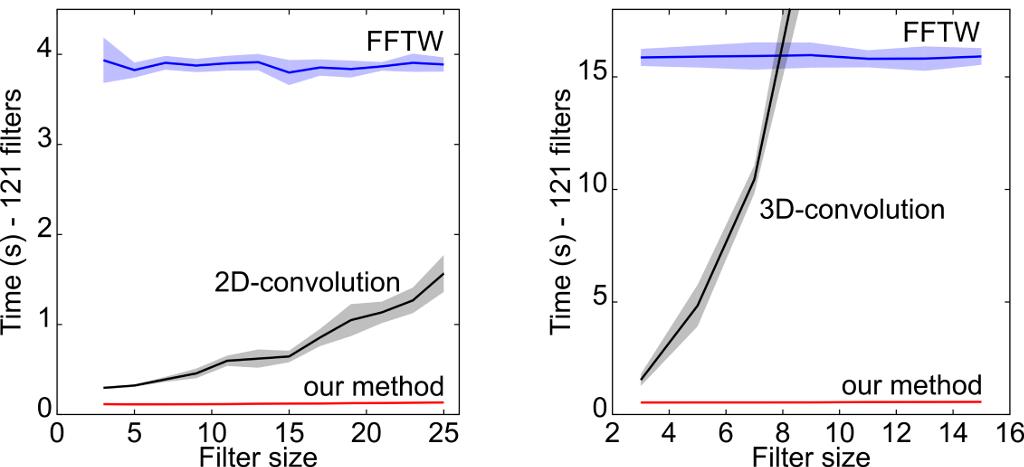
The computational costs linked with the use of a learned filter bank are, however, still considerable, as it requires the convolution with many non-separable filters.
We therefore present two strategies to deal with this issue in the context of the pixel classification problem:
- We use only few learned filters, leveraging the output of efficient hand-crafted approaches. This allows us to significantly reduce the number of filters — and therefore the time required for the convolutions — without sacrificing precision. Also, this has beneficial effects on the training time too, as learning few filters takes only some minutes compared to weeks of the traditional approach.
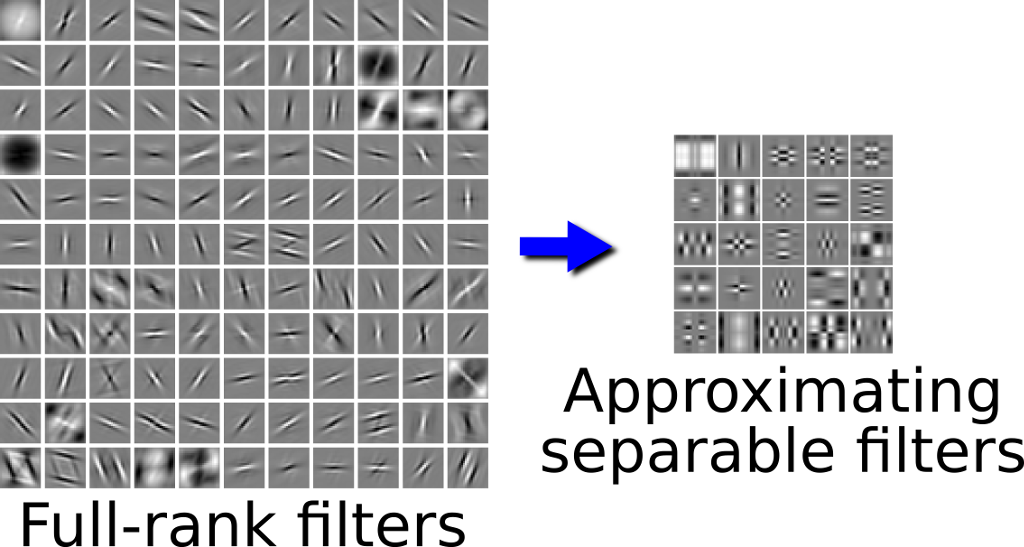
- We project the learned non-separable filter bank on a learned separable basis, making the computational costs of convolutions negligible with no loss in accuracy. We do this by approximating the full-rank filters using a smaller filter basis, where we impose the nuclear norm on each element to promote its separability.
Results
Our classification pipeline for the analysis of run-time sparsity.
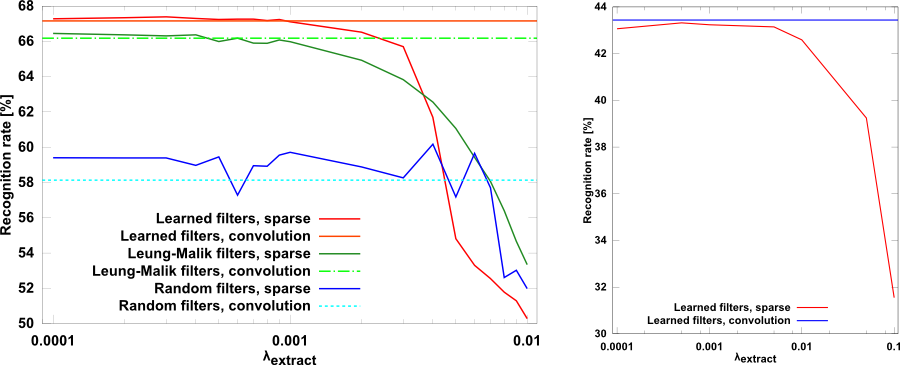
Classification rate as a function of sparsity on CIFAR-10 images downsampled to 16×16 pixels (left) and Caltech-101 images (right).Larger values for the regularization parameter correspond to sparser representations. From the graphs emerges that sparsity engenders no performance improvement in a convolutional architecture, which is good news as we can achieve good results with a reduced computational budget.
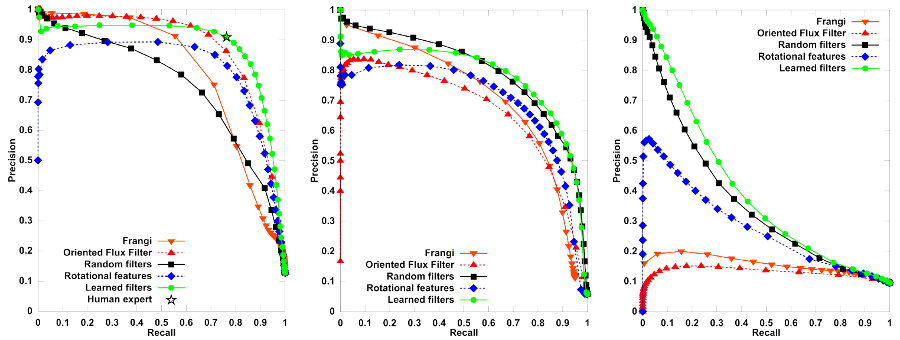
Precision/Recall curves for an image from the DRIVE (left), the BF2D (neurons) (center), and the Roads (right) datasets. Learned filters are compared with different handcrafted solutions, and score significantly better in the different situations. Comparing the results for different degrees of representation’s sparseness we observed that, as it was the case for image categorization, descriptors obtained by plain convolution perform at least as good as sparsified ones (see our technical report for further details).
These Precision/Recall curves show that, on very different datasets, there are no significant losses in accuracy when a large (121 filters) learned filter bank is replaced by a smaller one (9 filters) coupled with the output of two hand-crafted methods — in this case we have used the Enhancement Filter (EF) by Frangi et al. and the Optimally Oriented Filter (OOF). The results are averaged over the entire datasets and over multiple runs, and were obtained by a Random Forest (RF) classifier.
Software
To access the source code, please visit the accompanying software page.
References
Please note that the publication lists from Infoscience integrated into the EPFL website, lab or people pages are frozen following the launch of the new version of platform. The owners of these pages are invited to recreate their publication list from Infoscience. For any assistance, please consult the Infoscience help or contact support.
Are Sparse Representations Really Relevant for Image Classification?
2011. IEEE International Conference on Computer Vision and Pattern Recognition (CVPR 2011), Colorado Springs, p. 1545-1552. DOI : 10.1109/CVPR.2011.5995313.Please note that the publication lists from Infoscience integrated into the EPFL website, lab or people pages are frozen following the launch of the new version of platform. The owners of these pages are invited to recreate their publication list from Infoscience. For any assistance, please consult the Infoscience help or contact support.
Filter Learning for Linear Structure Segmentation
2011
Please note that the publication lists from Infoscience integrated into the EPFL website, lab or people pages are frozen following the launch of the new version of platform. The owners of these pages are invited to recreate their publication list from Infoscience. For any assistance, please consult the Infoscience help or contact support.
Accurate and Efficient Linear Structure Segmentation by Leveraging Ad Hoc Features with Learned Filters
2012. International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI), Nice, France, October 1-5, 2012. p. 189-197. DOI : 10.1007/978-3-642-33415-3_24.Please note that the publication lists from Infoscience integrated into the EPFL website, lab or people pages are frozen following the launch of the new version of platform. The owners of these pages are invited to recreate their publication list from Infoscience. For any assistance, please consult the Infoscience help or contact support.
Learning Separable Filters
2012
Please note that the publication lists from Infoscience integrated into the EPFL website, lab or people pages are frozen following the launch of the new version of platform. The owners of these pages are invited to recreate their publication list from Infoscience. For any assistance, please consult the Infoscience help or contact support.
Learning Separable Filters
2012
Contacts
| Roberto Rigamonti | [e-mail] |
| Amos Sironi | [e-mail] |
| Vincent Lepetit | [e-mail] |
| Pascal Fua | [e-mail] |