Extended tonality is a central system that characterizes the music from the 19th up to the 21st century, including styles like popular music, film music or Jazz. Developing from classical major-minor tonality, the harmonic language of extended tonality forms its own set of rules and regularities, which are a result of the freer combinatoriality of chords within phrases, non-standard chord forms, the emancipation of dissonance, and the loosening of the concept of key. These phenomena posit a challenge for formal, mathematical theory building. The theoretical model proposed in this paper proceeds from Neo-Riemannian and Tonfeld theory, a systematic but informal music-theoretical framework for extended tonality. Our model brings together three fundamental components: the underlying algebraic structure of the Tonnetz, the three basic analytical categories from Tonfeld theory (octatonic and hexatonic collections as well as stacks of fifths), and harmonic syntax in terms of formal language theory. The proposed model is specified to a level of detail that lends itself for implementation and empirical investigation.
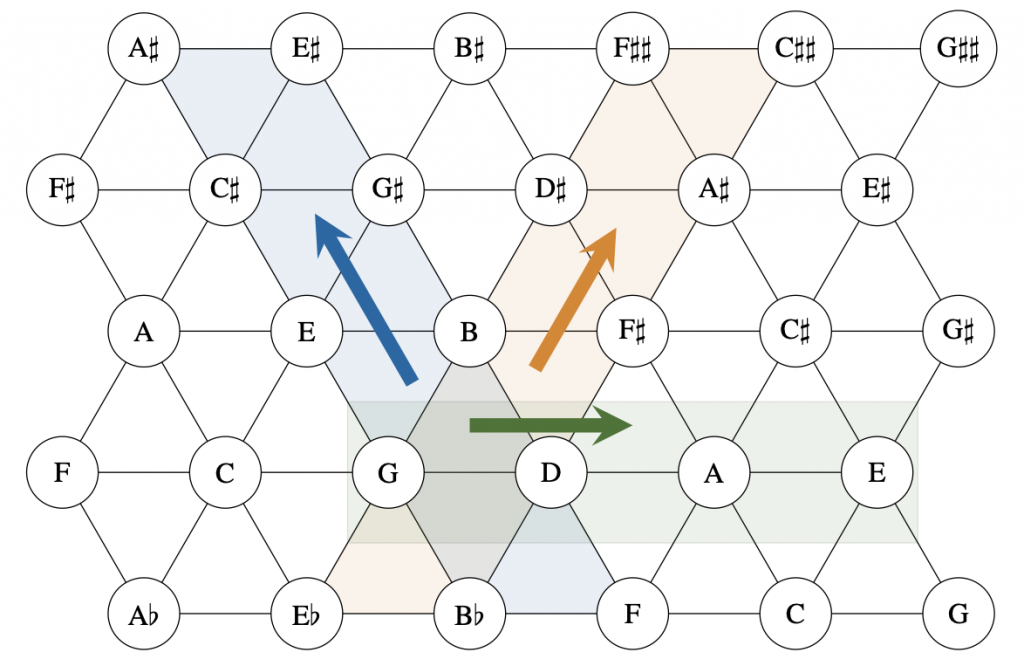
The foundation of our model lies in three different kinds of tonfelder, which are characerized using the three main axes of Euler’s tonnetz:
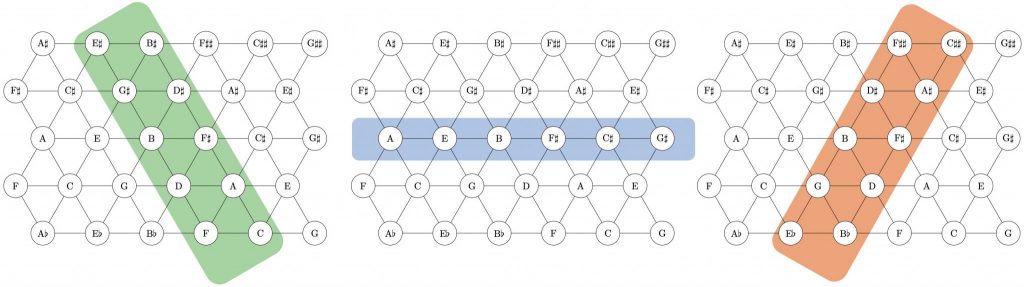
The model combines the three tonfelder with hierarchical syntactic analysis of harmonic sequences.
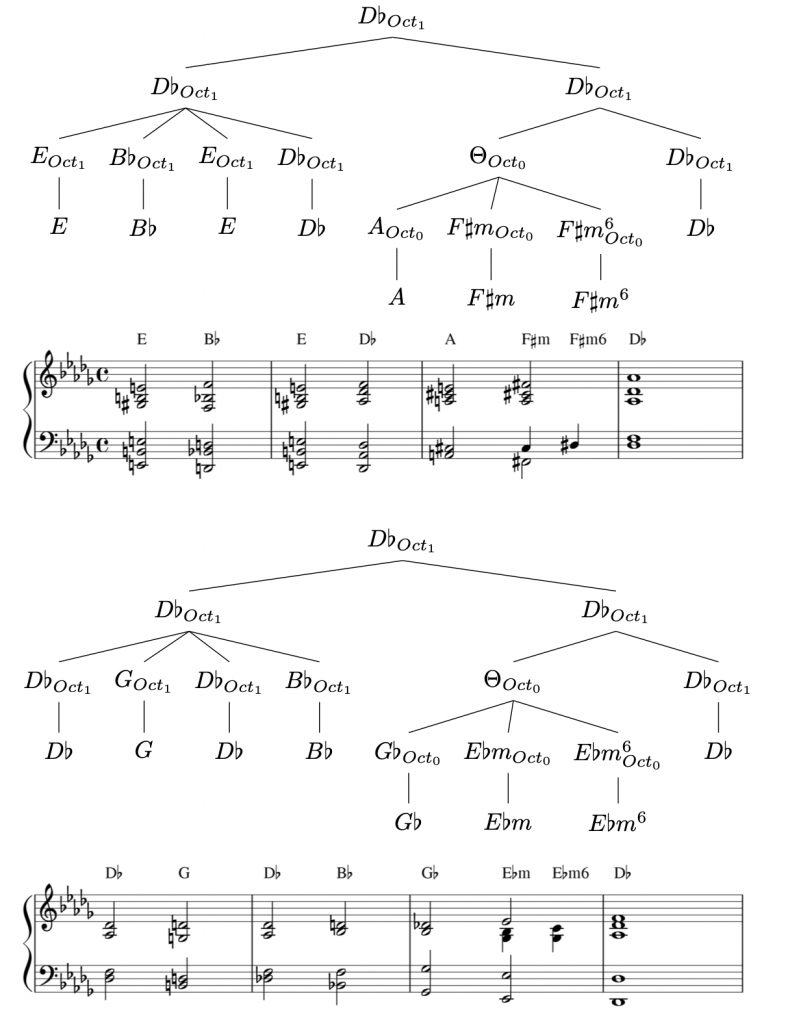
The following example displays an analysis of two phrases from the second movement of Antonin Dvorak’s 9th Symphony, mm.22–25 & mm.120–123. The analysis highlights that octatonic structures help to model this sequence of chords that cannot be accounted for within a single overarching diatonic key. The analysis also captures the very similar sounding of the two sequences despite their differences of the constituting chords: both sequences share the same overarching tree structure.
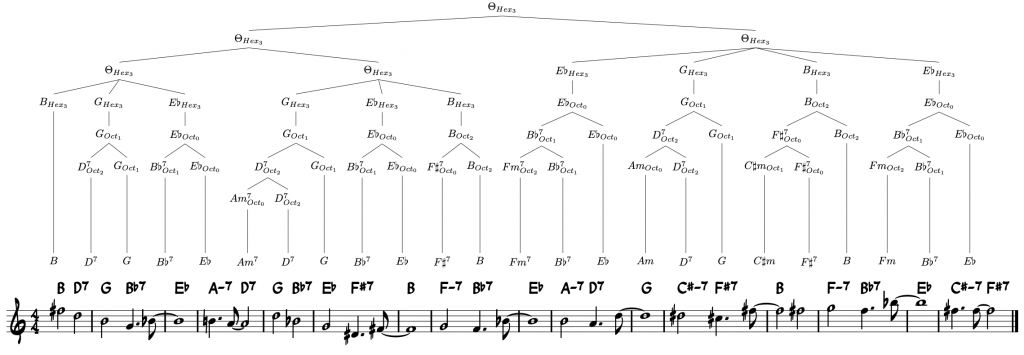
Another example illustrates how an overarching hexatonic structure could be employed in order to model very complex harmony such as in John Coltrane’s signature piece “Giant Steps”.
A final example illustrates how stacks of fifths could be employd to model cases of chord sequences such as Herbie Hancock’s “Maiden Voyage”. Notably, all of the sus-chords in the leadsheet refer to stacks of fifths and, further, the chords making up the A and B sections establish themselves overarching stack of fifths, both of which are in quasi-complement relation in the full circle of fifths.
