Recursive Bayesian Networks: A New Model Class for Describing Musical Structure ‒ DCML ‐ EPFL

A Recursive Bayesian Network with latent variables x and observed variables y. One specific possible structure is highlighted in blue, latent variables not included in the structure are shown in grey. The set of variables highlighed in orange and red are generated from the latent variable x0:3.

Structure of Johann Sebastian Bach’s Prelude No. 1 in C major, BWV 846, WTK I. (left): the colour indicates the most likely key at each point the the hierarchical structure. (right): the grey scale indicates the probability of the latent structure having a node at the corresponding location; the most likely structure is shown in red.

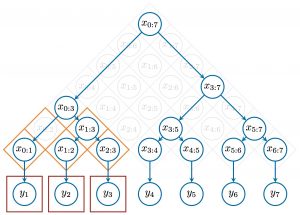
Musical form and syntax in Western classical music are hierarchically organised, similar to how sentences in natural language. Therefore some aspects of musical structure can be described with similar methods, such as with probabilistic context-free grammars (PCFGs) for chord symbols (where chords roughly take the role of words in language). However, beyond such a symbolic and discrete level, music has a rich and diverse level of gradual, sub-symbolic properties, such as how a chord is concretely expressed at the surface level (e.g. playing all chord tones at the same time or one after the other in an arpeggiation).

These sub-symbolic properties are highly challenging to capture with conventional hierarchical models. We therefore developed a new class of probabilistic models that build on the capacity of PCFGs for modelling hierarchical structure and combine it with that of dynamic Bayesian networks for representing continuous variables. The resulting class of Recursive Bayesian Networks allows us to model musical structure from the raw note level – a previously unsolved task in computational musicology.

Publication

Lieck R, Rohrmeier M (2021) Recursive Bayesian Networks: Generalising and Unifying Probabilistic Context-Free Grammars and Dynamic Bayesian Networks. In: Advances in Neural Information Processing Systems 34: Annual Conference on Neural Information Processing Systems 2021

Acknowledgments

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No 760081 – PMSB. This project was conducted at the Latour Chair in Digital and Cognitive Musicology, generously funded by Mr. Claude Latour.