It is almost trivial to state that composers from different times write music in very different styles. But how can aspects of this stylistic differences be investigated on a larger scale? How can we study whether there are systematic changes in the way music evolves throughout time? Traditional music theorists address questions like these by producing detailed analyses of musical pieces that they deem somewhat representative for a certain period. By observing different patterns, e. g. in the way notes are used and combined to harmonies, one can pin down major steps in the historical development of music.
But this approach has a few setbacks: How can one be sure that the chosen pieces are indeed representative and not merely special cases that analysts deemed interesting? Several projects within the Digital and Cognitive Musicology Lab‘s corpus initiative address this caveat by gathering, digitizing, curating, and studying large amounts of musical pieces with empirical and computational methods.
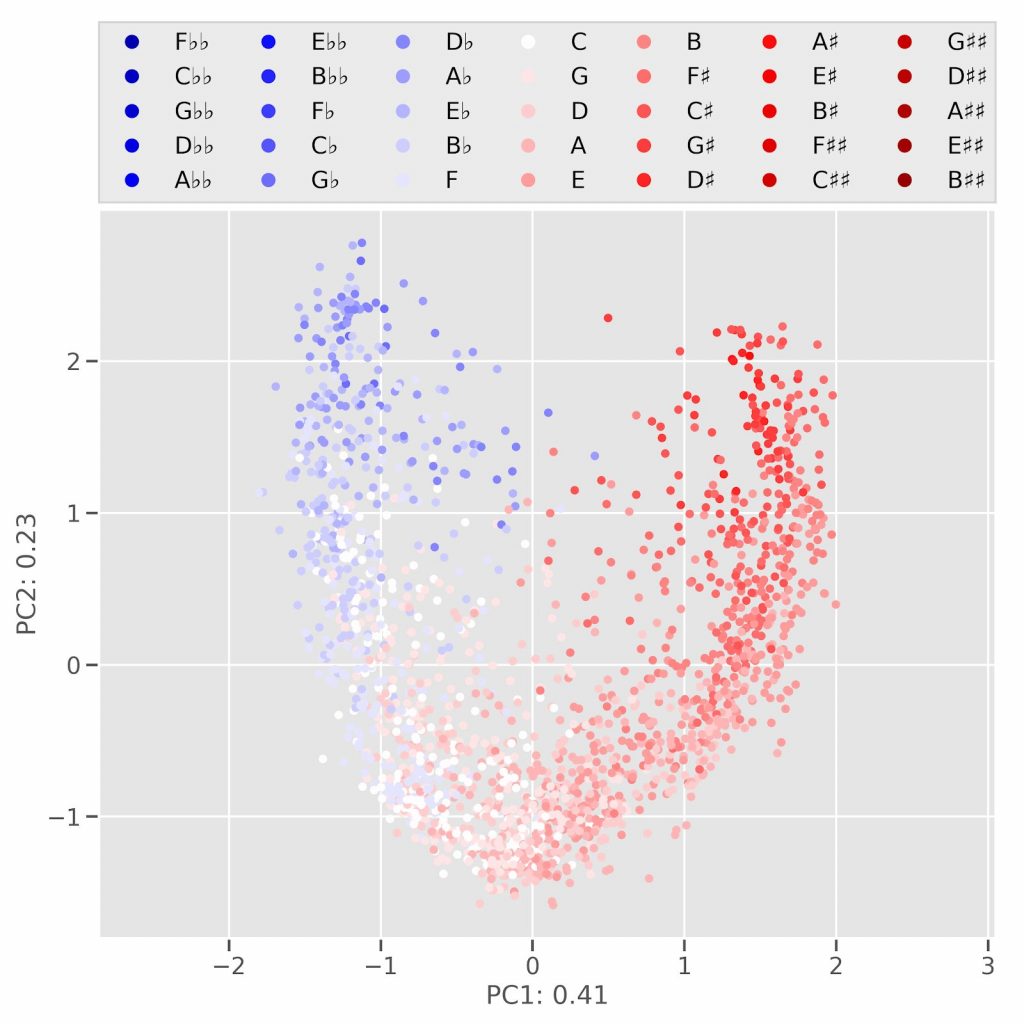
A central music-theoretical area of study is the implicit theoretical models that composers employ when they write music. In other words, how do they combine notes in their pieces and which general principles do they follow – consciously or not. In order to study this, we applied a variety of methods from statistics and machine learning called dimensionality reduction to a large corpus of more than 2000 pieces by 75 composers, covering more than 600 years of Western musical history. If there was a consistent underlying structure for all of these pieces that could largely account for the notes in the pieces despite their great diversity, this would mean that we would have uncovered a fundamental structuring principle that holds for virtually all compositions of Western classical music.
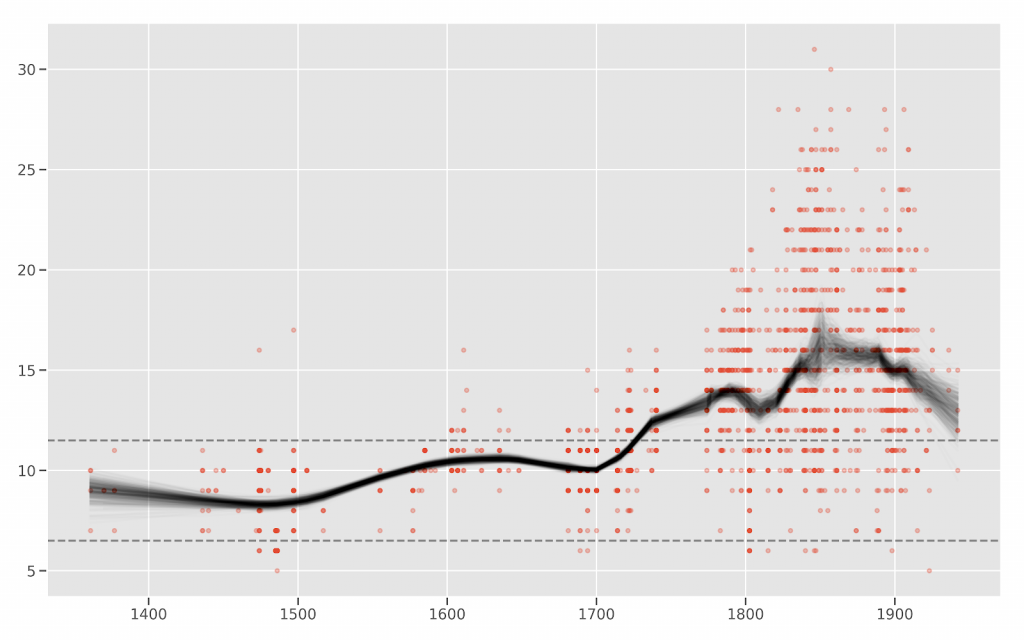
The results were astonishing. Not only could we recover the so-called line of fifths (Figure 1) without assuming its existence in the first place, we could moreover show that, over the course of history, composers explore ever wider ranges on this line (Figure 2).