| Professeur | Prof. Friedrich Eisenbrand |
| Assistants | Adrian Bock |
| Marco Di Summa | |
| Martin Niemeier | |
| Laura Sanità | |
| Langue | Français |
Actualités
- L’information pour l’examen est disponible ici.
- Les corrigés des examens blancs sont en lignes.
- Des examens blancs sont en lignes.
- Les transparents et la série du 19 mai sont disponibles.
- Les notes de cours sont mises à jour.
- Les transparents et les séries du 12 mai sont disponibles.
- Les corrigés de la série 9 et d’EPFLove sont en lignes.
- Les transparents et la série du 5 mai sont disponibles.
- La condition d’un couplage stable a été corrigée dans l’exercice EPFLove.
- Les notes de cours en anglais sont mises à jour.
- La série 9 et le corrigé 6 sont mis à jour. Une liste des exemples pour EPFLove est en ligne.
- Les transparents et les séries du 21 avril sont disponibles.
- La série 8 est mise à jour.
- Les transparents et la série du 14 avril sont en ligne.
- Le matériel du cours est mis à jour.
- Les transparents et la série du 7 avril sont disponibles.
- Le code SAGE pour l’exemple de la phase I de l’algorithme du simplexe est disponible.
- Le corrigé de la série 5 est en ligne.
- Les transparents et la série du 31 mars sont en ligne.
- Les transparents, la série et les notes de cours sont mis à jour après le cours du 24 mars.
- La série 5 est en ligne.
- Les transparents du 24 mars sont disponibles.
- Les notes de cours en anglais sont mises à jour.
- L’historique de SAGE utilisé pendant le cours est disponible.
- Le corrigé de la série 3 est en ligne (sauf l’exercice SAGE, bien sûr)
- La série 4 est mise à jour.
- Les transparents et la série du 17 mars sont disponibles.
- Le corrigé de la série 2 est en ligne.
- Les transparents et la série du 10 mars sont disponibles.
- Il y a des indications supplementaires pour le mode d’exercices.
- Les horaires de bureau sont annoncés.
- Les transparents et la série du 3 mars sont disponibles.
- Les transparents et la série du 24 février sont en ligne.
Objectifs
Familiariser les étudiants avec des modèles de programmation linéaire et des algorithmes. Leurs apprendre à développer et analyser des algorithmes.
Contenu
Algorithme du simplexe
Perturbations et règle lexicographique
Lemme de Farkas et dualité
Méthode duale du simplexe
Polyèdres
Couplages et flots dans les réseaux :
Couplage biparti et non-biparti
Polytope de couplage.
Examen et la note finale
Il y aura un examen écrit à la fin du semestre.
Le calcul de la note finale N à partir du bonus B et du pourcentage P de points obtenus à l’examen est fait par la formule suivante
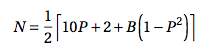
Le bonus est le pourcentage des exercices corrects.
Horaires
Cours : Jeudi, de 10h15 à 12h, Auditoire MA11
Séances d’exercices : Jeudi, de 12h15 à 13h, Auditoire MA11
| Lundi 14-15 | Prof. Eisenbrand |
| Lundi 17-18 | Martin Niemeier |
| Mardi 12-13 | Laura Sanità, Adrian Bock |
| Mercredi 12-13 | Marco Di Summa |
Matériel du cours
Vous trouvez ci-dessous les transparents utilisés dans le Cours. La version à imprimer vous permet de prendre des notes pendant le Cours. Il est donc fortement conseillé de l’imprimer en avance.
| Partie | Chapitre | À regarder | À imprimer | Version | Remarques |
|---|---|---|---|---|---|
| Programmation linéaire | Exemples | Cours_01 | Cours_01 | 25.02. | correction des erreurs: x2 sur les premiers transparents, PL de la boule adjusté |
| Systèmes linéaires | Cours 02 | Cours 02 | 09.03. | mise à jour des transparents après le cours. Derniers transparents remis à la semaine prochaine. | |
| L’algorithme du simplexe | Cours 03 | Cours 03 | 16.03. | petite faute corrigée, notation modifiée | |
| L’algorithme du simplexe (2) | Cours 04 | Cours 04 | 17.03. | Exemple SAGE modifié | |
| L’algorithme du simplexe (3) | Cours 05 | Cours 05 | 24.03. | mise à jour des transparents après le cours. | |
| Dualité | Cours 06 | Cours 06 | 30.03. | ||
| Dualité (2) | Cours 07 | Cours 07 | 08.04. | mise à jour des transparents après le cours. | |
| PL en nombres entiers | Cours 08 | Cours 08 | 15.04. | Coquilles corrigées | |
|
|
Algorithmes | Cours 09 | Cours 09 | 20.04. | |
| L’éfficacité de l’algorithme du simplexe | Cours 10 | Cours 10 | 05.05. | mise à jour après le cours. | |
| Couplages et flots dans les reseaux | Graphes | Cours 11 | Cours 11 | 12.05. | mise à jour après le cours. |
| Réseaux et Flots | Cours 12 | Cours 12 | 19.05. | Coquilles corrigées |
Vous trouvez ici des notes de Cours (11.05.) en anglais.
Code SAGE utilisé pendant le cours :
03.03. L’élimination de Gauss-Jordan (Historique)
17.03. L’algorithme du simplexe (Historique, Fonctions auxiliaires)
05.04. Exemple de la phase I de l’algorithme du simplexe (Code SAGE)
Examens blancs: EB1 corrigé EB2 corrigé
Exercices
| Séries Solutions |
|---|
| série 01 corrigé 01 |
| série 02 corrigé 02 |
| série 03 corrigé 03 |
| série 04 corrigé 04 |
| série 05 corrigé 05 |
| série 06 (Ex. 2 mis à jour) corrigé 06 |
| série 07 corrigé 07 |
| série 08 (Ex. 3 mis à jour) corrigé 08 |
| série 09 corrigé 09 |
| série 10 corrigé 10 |
| série 11 corrigé 11 |
| série 12 corrigé 12 |
- Gauss-Jordan exemple corrigé
- Algorithme du simplexe: étape iii) corrigé
- Algorithme du simplexe exercice corrigé
- EPFLove exercice corrigé exemple
- Arbitrage exercice corrigé exemple
- Le corrigé sera disponible dès lors que vos rendus sont tous examinés.
- Le bonus est attribué de manière 0/1, c’est-à-dire on obtient 1 point pour un exercice si la solution rendue est correcte en majorité et 0 si non.
Références
Jiří Matousek and Bernd Gärtner. Understanding and using linear programming. Springer, 2006. ISBN 978-3-540-30697-9 (bibliothèque, en ligne (accessible seulement depuis le reseau de l’EPFL))
Stephen Boyd and Lieven Vandenberghe. Convex Optimization. Cambridge University Press, 2004. ISBN 0521833787 (disponible en ligne)
Jean-François Hêche, Thomas M. Liebling, Dominique de Werra, Recherche opérationnelle pour ingénieurs I (bibliothèque)
Dimitris Bertsimas and John N. Tsitsiklis. Introduction to linear optimization. Athena Scientific, 1997. ISBN 1-886529-19-1
Ravindra K. Ahuja, Thomas L. Magnanti, James B. Orlin. Network flows : theory, algorithms, and applications. Prentice Hall, 1993. ISBN 0-13-617549-X
Thomas Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein. Introduction à l’algorithmique. MIT Press, 2004. ISBN 978-0262032933 (bibliothèque, site web)