Background: Rayleigh-Bénard Convection (RBC), a system where fluid between two infinite plates is heated from below, is a canonical system to study “routes to chaos” (small-scale convection) and “pattern formation” (large-scale convection). Both research problems consider the emergence of new solutions under the change of system parameters like temperature difference or aspect ratio. Over the last decades, scientists have studied the emerging solutions with linearization and reduction techniques. Our numerical tools provide access to exact fully non-linear 3D invariant solutions even if they are dynamically unstable. This way, we can calculate full bifurcation diagrams of 3D convection solutions.
Convection rolls in RBC do not move into a preferred direction. If the convection cell is inclined against gravity, solutions can start to drift down or up the inclination although the base flow does not provide a net flux. Experiments of ILC by Daniels et al. (2000) show for example drifting transverse rolls. First results with our code show a travelling wave solution even for smallest inclinations (see Figure).

Objective: Follow 3D tertiary (or higher) states of RBC into the inclined convection regime and see if they start to drift or not. Relate the onset of drift to symmetry breaking and characterize the phase velocities of these travelling waves.
Main questions:
- How do RBC-solutions behave under inclination? Which drift? Which do not drift?
- Can we understand the drift velocity?
Requirements:
- Basic knowledge of unix and C++,
- Having passed “ME 467 Turbulence” and ideally “ME 466 Instability”
Learning outcome:
- Understanding the physics of the fundamental convection system,
- Algorithms to find exact fully-nonlinear solutions,
- Symmetry arguments,
- Operating an MPI-code on HPC clusters
- Working at the frontier of research
Background: Thermal convection in a fluid between a lower hot plate and an upper cold plate becomes turbulent if the temperature difference, parametrized by the Rayleigh number Ra, is large (Ra>>10^3). In turbulent convection, the transport of heat between hot and cold plate scales with Ra as a power law. The precise form of this power law is subject to current research involving theory, numerical simulations and experiments.
This project uses a state-of-the-art approach of finding exact fully non-linear 3D solutions of thermal convection that are stationary in time and represent building blocks of turbulent dynamics. These steady solutions have precise heat transport properties (cheap to calculate) which are compared with the transport statistics of fully turbulent flow (expensive to calculate). The main goal of this project is to find invariant solutions which optimize heat transport and follow the predicted scaling laws. A recent study has done this in 2D (Waleffe et al., 2015). We can do it in 3D (see Figure). The same approach is of interest for the convection in a vertical gap.
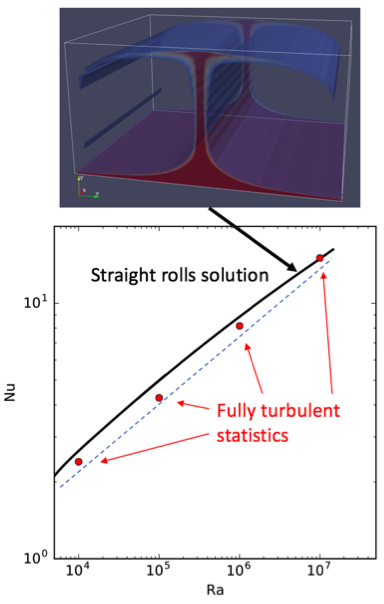
Objective: Compare the Ra-scaling of the normalized heat transport, given by the Nusselt number Nu, of 3D tertiary (or higher) states of RBC with DNS statistics of turbulent convection. Try to make contact with theoretical scaling law predictions.
Main questions:
- How do invariant solutions transfer heat compared to statistical fluctuations?
- How do invariant solutions scale over Ra compared to statistics?
- Until what Ra is the Boussinesq approximation, used in the governing equations, reasonable to study heat transfer?
- What are optimal heat transport solutions?
Requirements:
- Basic knowledge of unix and C++,
- Having passed “ME 467 Turbulence”
Learning outcome:
- Understanding the physics of a fundamental fluid system,
- Algorithms to find exact fully-nonlinear solutions,
- Turbulence theory of convective flows,
- Operating an MPI-code on HPC clusters,
- Working at the frontier of research
Invariant solutions of Navier–Stokes equations in a boundary layer flow
Turbulent boundary layer flows are characterized by coherent structures in a vast range of scales. Among all these coherent structures, streaky motions contain most of the energy in the flow. Both small-scale streaks near the wall and large-scale streaky motions in the boundary layer are important elements of a turbulent boundary layer flow. The small-scale streaks are located close to the wall and control the wall shear and the large-scale motions are responsible for most of the momentum and energy transfer in the flow. The aim of this project is to find exact invariant solutions of the Navier-Stokes equations which can represent the dynamics of these streaky structures in a boundary layer flow. Numerous exact invariant solutions of the Navier-Stokes equations have been found in the transitional regime in wall-confined periodic channel flows such as plane Couette flow which is a shear-driven flow between two parallel plates that move in opposite directions. The idea of this project is to take these solutions to high Reynolds number boundary layer flows and to see whether they are connected to the streaks near the wall or to the large-scale motions in the outer layer. The method of homotopy is the main tool to carry out this transition from plane Couette flow to the boundary layer flow. In the method of homotopy, the boundary conditions are slowly changed so that the system finally becomes a new system (Look at the GIF as an example). Here, the target system is asymptotic suction boundary layer flow (ASBL) which is a boundary layer over a flat plate with suction into the plate. ASBL is a simple boundary layer flow which has many applications both in science and industry, as suction is a way to suppress turbulence in a boundary layer flow. After the exact invariant solutions are transferred to ASBL, we will use filtering methods to see if they are connected to large-scale motions in the outer layer or small-scale streaky structures next to the wall.

Objective: Find exact invariant solutions of Navier-Stokes equations which can represent the dynamics of streaky motions in a boundary layer flow
Main question: Is there any connection between exact invariant solutions of Navier – Stokes in confined channel flows and streaky motions in boundary layer flows?
Requirements:
- Basic knowledge of unix and C++,
- Having passed “ME 467 Turbulence”
Learning outcome:
- The method of Homotopy
- A filtering method
- Algorithms to find fully nonlinear solutions
- Symmetry arguments
- Operating an MPI code on HPC clusters
- Working at the frontier of research
Background: Unstable periodic orbits (UPOs) are believed to be the dynamical building blocks of spatio-temporal chaos as they provide key insights into the dynamics and the structure of the chaotic attractor. The identification of UPOs in PDE systems remains challenging though. Typically this process is done in steps: first defining an initial guess for the UPO, and then secondly using a convergence algorithm to converge the guess to a solution of the system. This study is concerned with the first step for a particular type of convergence algorithm (Azimi et al. 2022), where guesses are closed curves (loops) in state space that are deformed until they satisfy the governing equations. The goal of this project is to develop a data-driven method to produce loop guesses for the 1D Kuramoto-Sivashinsky PDE.
Data from a numerical simulation of the system is mapped to a low-dimensional ‘latent space’ using an autoencoder neural network. The resulting latent space is separated into clusters, and guesses for periodic orbits are generated based on the transition probabilities between clusters.
Objective: Developing a data-driven method for generating loop guesses for unstable periodic orbits.
Main questions:
- How can we separate the chaotic attractor into meaningful clusters?
- How can we leverage the transition probabilities between these clusters to generate guesses for UPOs?
Requirements:
- Basic Python knowledge.
- Basic Dynamical Systems knowledge
- Having passed “ME 467 Turbulence”.
- Bonus: Basic Probability and Machine Learning knowledge.
Learning outcomes:
- Understanding the importance of UPOs in spatio-temporal chaos.
- Understanding of various concepts in dynamical systems, probability and machine learning.
- Algorithms to find exact fully-nonlinear solutions.
- Working at the frontier of research.
