Buckling analysis of arcs using a local probing technique
Background: Reconsidering the classical buckling problem within the framework of dynamical system theory, a basin of attraction is defined for the unbuckled state, while a basin boundary exists between the unbuckled and buckled states and edge states, as saddle points, are embedded in the basin boundary.
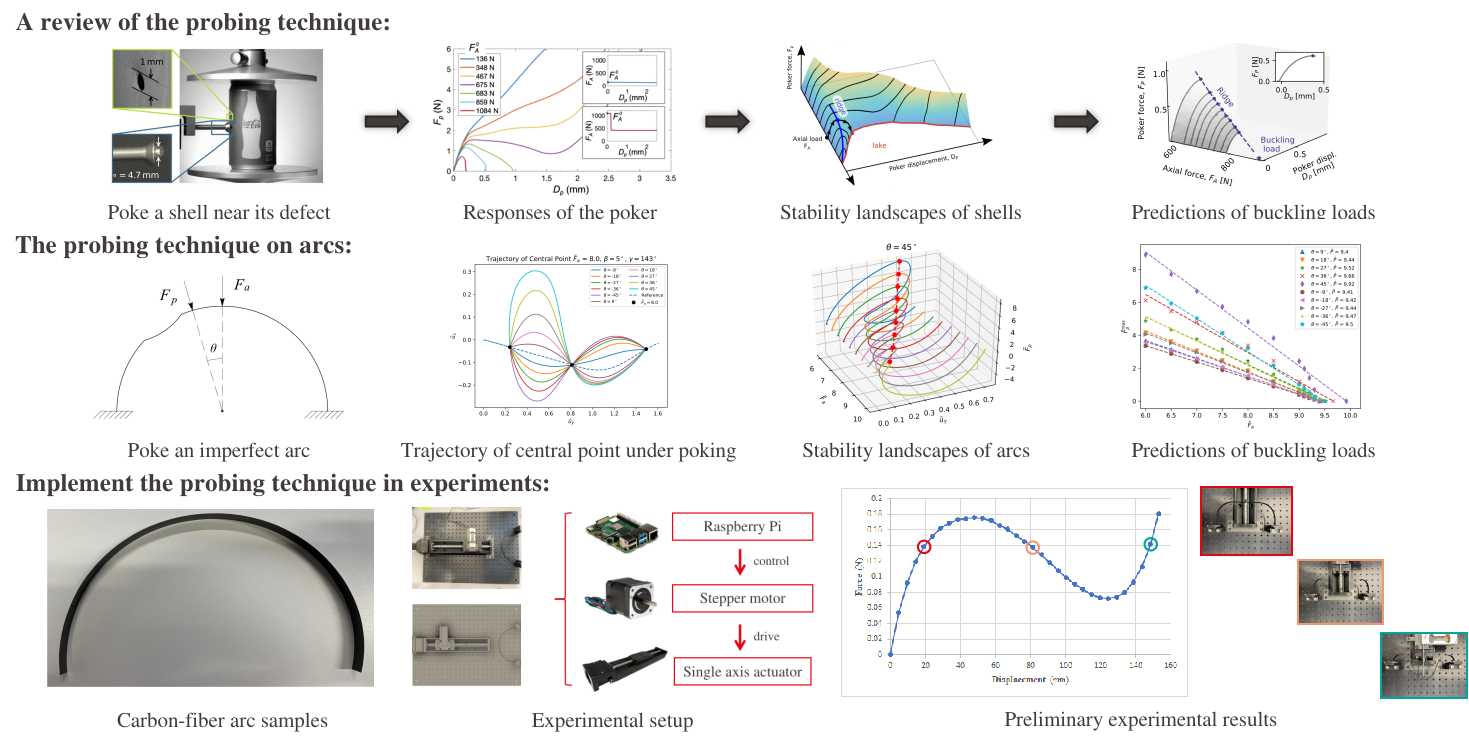
Recently, a novel probing technique has been developed by scientists based on this concept, which uses an additional poker as a finite-amplitude perturbation to the original system. The system is forced to leave the unbuckled state and cross the basin boundary under the poking force. By tracking the ridge of the stability landscape, which indicates the size of the basin as a function of load, one can predict the spontaneous buckling load by extrapolation non-destructively.
However, this probing technique only works under limited conditions, which are still not fully clear by far. In this project, we focus on the arc buckling problem that a clamped semi-circular arc buckles under a point force, most experimentally, to analyze the role of the probing technique systematically.
Objectives:
- Investigate the influence of imperfections on the edge state of arcs
- Acknowledge the conditions when the nondestructive probing technique is successful.
Experimental and Numerical tools:
- Carbon-fiber arcs; Single axis actuators; Load cells, Raspberry Pi; 3D printers.
- A home-made FEM code based on the Reissner-Simo beam model.
Contact: tian.yang@epfl.ch