Superconducting devices

Coming soon.
High-Kinetic Inductance superconducting devices

Coming soon.
Coming soon.
Coming soon.
cQED with Semiconductor Quantum Dots on planar Ge and GaAs
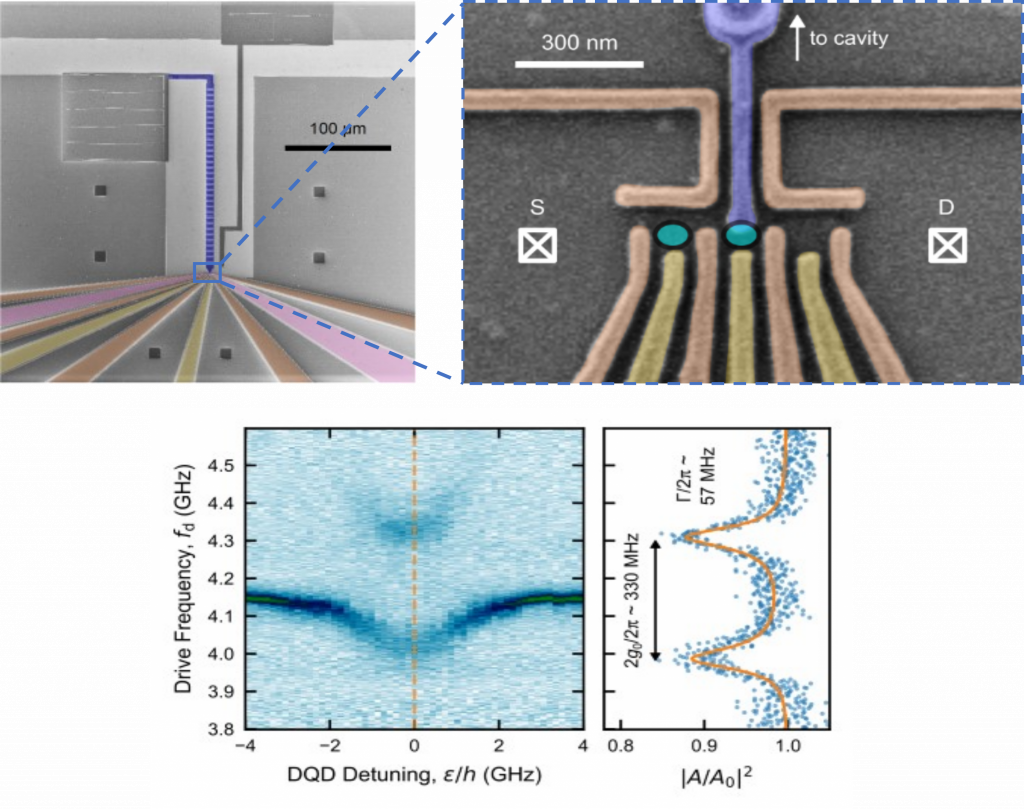
In the strong coupling regime, the vacuum Rabi mode splitting is observed if the coupling strength g is higher than the total system decoherence 1. Achieving the strong coupling regime with microwave radiation has been proved to be challenging for QDs due to their usual high decoherence rates and limited coupling strength. Our strategy to reaching the strong coupling limit is rooted in enhancing the electric component of the electromagnetic field’s vacuum fluctuations obtained by increasing the resonator impedance Zr beyond the typical 50 Ω of conventional coplanar waveguides2,3 (g2 ∝ Zr ). This approach is universally applicable to any circuit QED system striving to maximize the coupling strength.
A high impedance resonator can be defined by arrays of Josephson junctions. A Josephson junction (JJ) is formed by two superconducting electrodes separated by a thin insulating tunnel barrier. The Josephson inductance LJ = Φ0 / (2π Ic cos φ) depends on the superconducting phase difference across the junction φ. Here Φ0 is the magnetic flux quantum and Ic the critical current of the junction. Connecting two JJs in parallel forms a superconducting quantum interference device (SQUID) (depicted in Fig.1d), which is nonlinear and non-dissipative but exhibits a tunable critical current that depends periodically on the externally applied magnetic flux penetrating the SQUID loop. JJs and SQUIDs are circuit elements that provide a high inductance at small dimensions, making them ideal building blocks for assembling high impedance resonators.
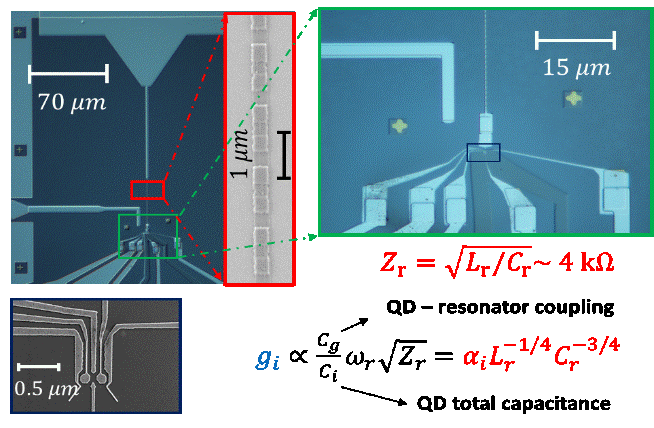
A different class of high-impedance superconducting microwave resonators is based on the high kinetic inductance of niobium-titanium nitride (NbTiN)2, niobium nitride (NbN)20, titanium nitride (TiN)21, and granular aluminum22 disordered superconducting thin films. By creating a resonator from a superconducting wire of thickness lower than 10 nm, a width of 100 nm, and length of 300 µm, from a film with a kinetic inductance of 100 pH/square, one can define a very compact Lr ∼1 µH inductor. The kinetic inductance can be made about 1000 times higher than the typical geometric inductance, which allows us to define, for a chosen resonance frequency, a resonator with a length about 33 times shorter. By taking advantage of the high kinetic inductance, it is possible to increase Zr by about two orders of magnitude compared to standard CPW resonators. The corresponding voltage vacuum fluctuation is expected to provide a single photon-electron coupling ten times stronger than the one achievable with conventional microwave transmission line resonators.
Simultaneously to our experiment using a DQD coupled to a SQUID array resonator in GaAs3, other two independent works demonstrated the strong coupling regime by making use of a DQD in SiGe4 and of a QD build in a carbon nanotube with superconducting leads5, both coupled to a standard 50 Ω CPW resonator.
Right after the demonstration of the strong coupling regime, the development of circuit QED employed to couple semiconductor QDs has matured very rapidly to the extent that several important results have been demonstrated over the last couple of years.
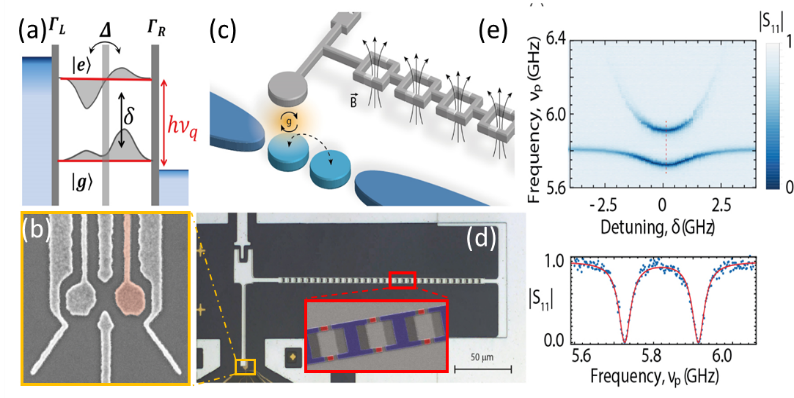
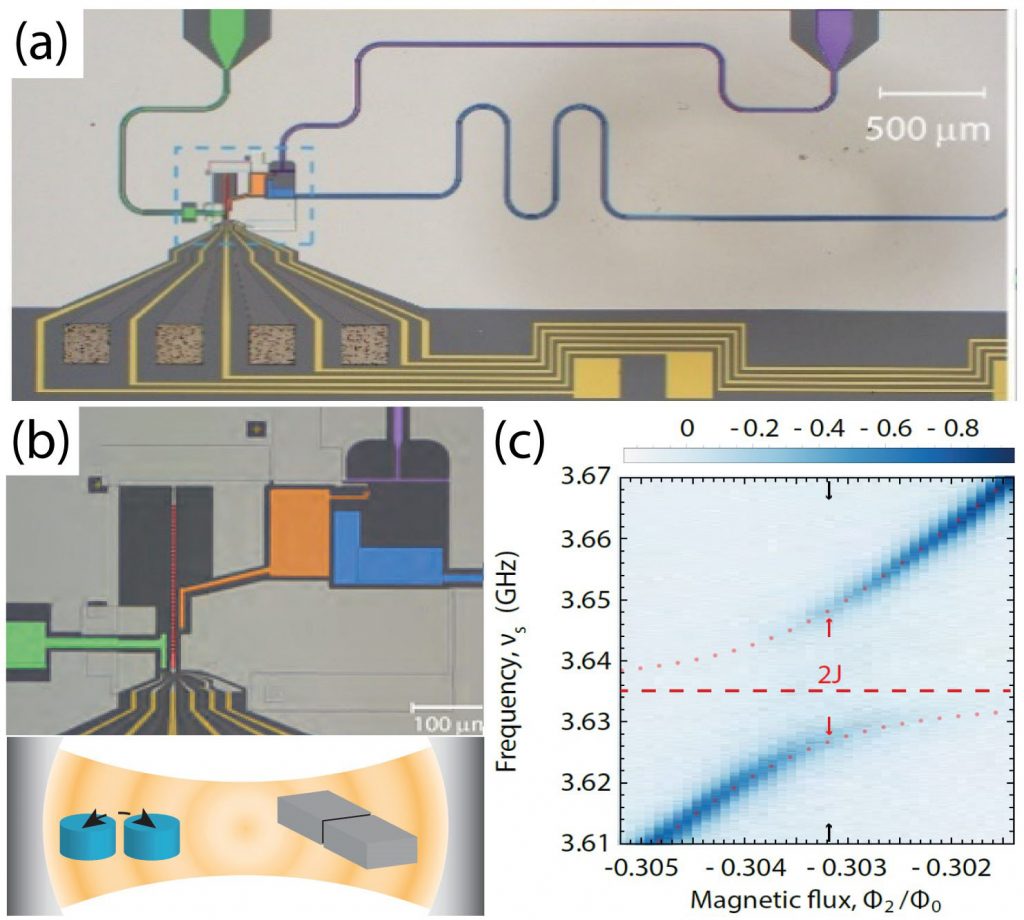
Recently, simultaneously with TU-Delft6 and Princeton7 groups, during my postdoc activity at ETH Zurich, we managed to reach the strong coupling between an electron spin system in GaAs and microwave photons8 (see Fig.2). This represented a significant milestone toward the development of a spin-based or hybrid quantum processor9. In our experiment8, the strong coupling has been demonstrated between a single microwave photon in a high impedance NbTiN cavity and a three-electron resonant exchange spin-qubit defined in a GaAs triple QDs. While not yet demonstrated, virtual-photon-mediated spin-spin coupling is within experimental reach10 with further improvements in resonator quality factors, spin-photon coupling rates, and further suppression of noise-induced dephasing. Coupling long-distance spins is still a crucial missing element towards quantum information processing9.
We recently realized a device that integrates a QD-based (charge11 and spin12) qubit with a superconducting transmon qubit, both strongly coupled to a tunable high impedance SQUID array resonator, acting as a quantum bus (see Fig.3). A coherent superconductor-semiconductor interface enables both charge/spin and charge/flux degrees of freedom in the same device. The addition of a transmon to such an experimental setup provides several exciting new opportunities. For instance, it could be used as a noise-sensitive spectrometer and give more insight into quantum dot circuits’ properties.
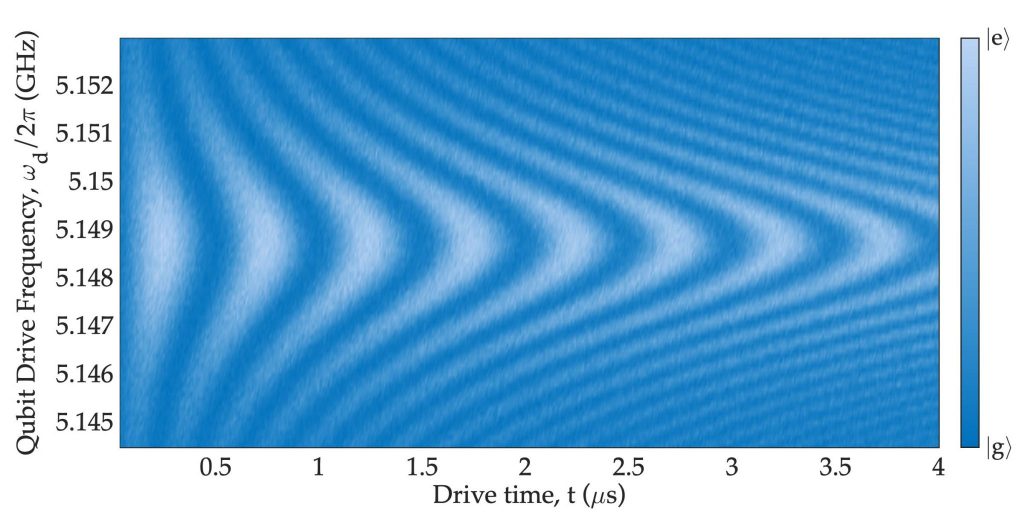
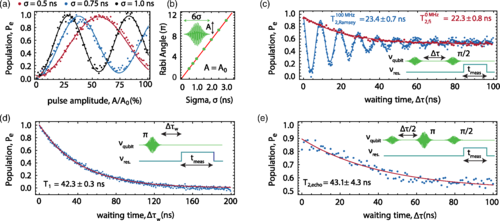
Achieving the strong coupling limit of cavity QED allowed using a microwave resonator to efficiently read-out dispersively, in the time domain, a resonantly driven GaAs DQD charge system. The work reported in ref.14 represents the first time-resolved comprehensive study of the coherence properties of a DQD charge qubit realized in a cQED architecture, and it has been enabled by the improved coherence of the DQD charge system. These results inevitably trigger some new fundamental questions regarding the optimization of device parameters (size of the QDs, gates design) to increase even further the QDs’coherence.
[PRL 122, 206802 (2019)].
Recently, we developed a strategy to systematically modifying in-situ the magnitude of the DQD electric dipole moment (see Fig.7), which controls both the coupling strength with the superconducting resonator and the qubit decoherence15. This method relies on exploring different configurations of the DQD confinement potential created by the surface metallic gates. This tuning strategy allows engineering the charge qubit decoherence rate down to ~2 MHz in GaAs14. These rates are expected to reduce further by moving to Si or Ge systems4,17. We anticipate that these findings will be of great significance for the state-of-the-art charge and spin qubits and any hybrid designs, all of which are currently limited by charge noise. Although a DQD charge-based system is more prone to decoherence processes (if compared to superconducting transmon qubits) given its higher coupling to external charge noise sources, we plan to investigate a limit where the artificial atom is ultrastrongly coupled17,18 to the cavity, which will be the dominant source of dissipation. In the USC regime, the rotating-wave approximation (RWA) used in the Jaynes–Cummings model breaks down, and the system should be described by the complete quantum Rabi model17,18. The onset of the USC regime for a DQD has been obtained for a DQD configured to maximize its electric dipole moment, coupled to a Josephson junction array resonator19.
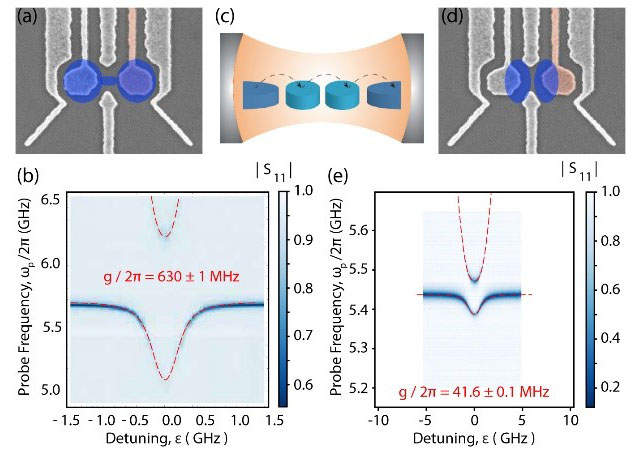
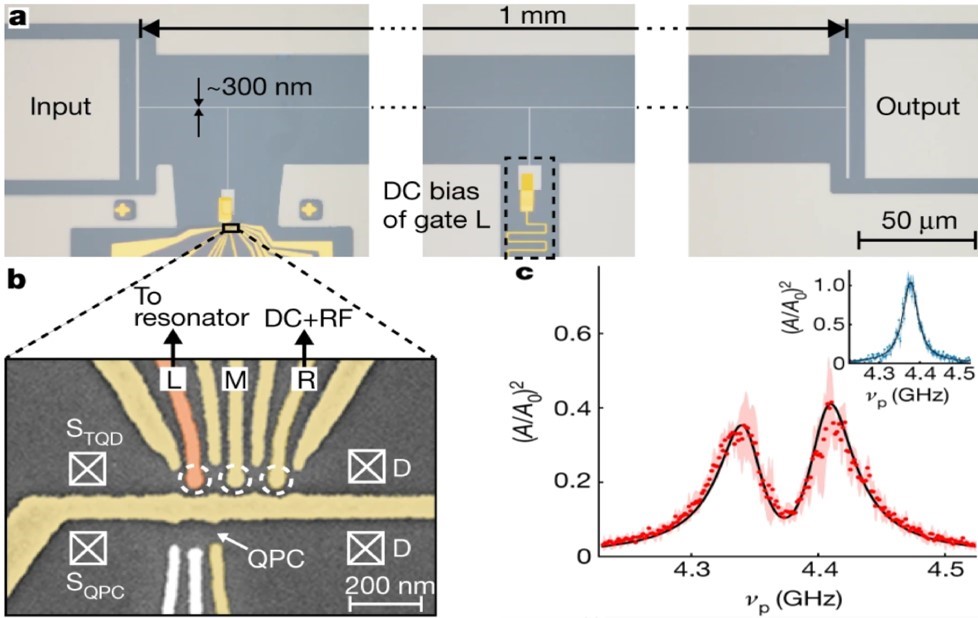
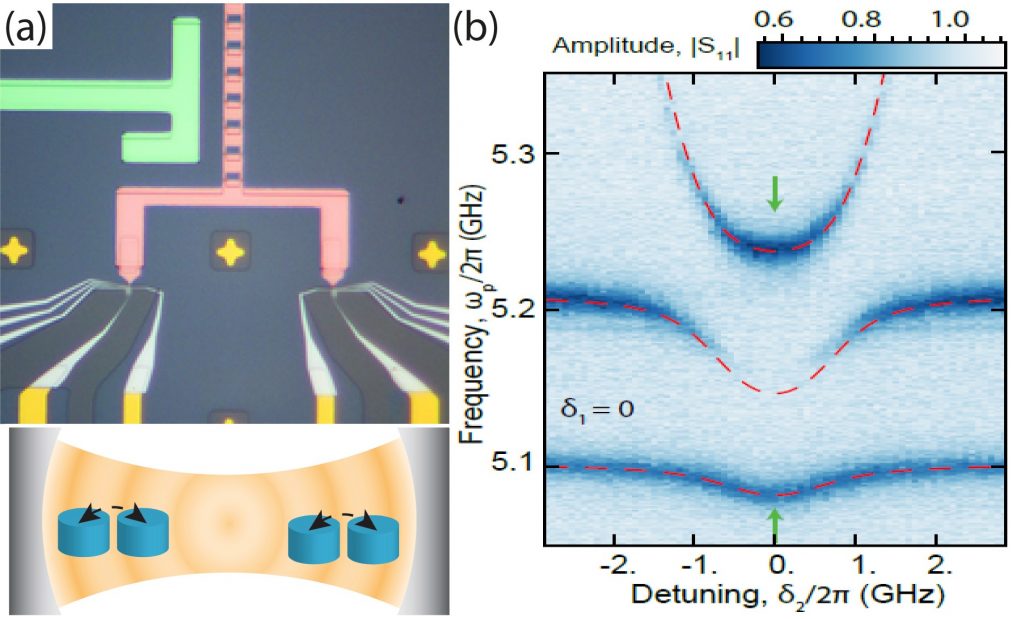
The cQED approach is also of primary importance as a means for scaling semiconductor QDs-based architecture9. We implemented a first device prototype (see Fig.4), consisting of two depletion DQDs defined in a GaAs 2DEG and separated about 45 µm13. Both DQDs are capacitively coupled to the same side of a high impedance SQUID array resonator, which mediates the coherent interaction between them. This technique provides a “copy-and-paste” scheme for adding qubits to an existing network, thus potentially mitigating the scaling problem that typically plagues platforms based on QD-based qubits.
References
- Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004).
- Samkharadze, N. et al. High-Kinetic-Inductance Superconducting Nanowire Resonators for Circuit QED in a Magnetic Field. Phys. Rev. Applied5, 044004 (2016).
- Stockklauser, A. et al. Strong Coupling Cavity QED with Gate-Defined Double Quantum Dots Enabled by a High Impedance Resonator. Phys. Rev. X 7, 011030 (2017).
- Mi, X., Cady, J. V., Zajac, D. M., Deelman, P. W. & Petta, J. R. Strong coupling of a single electron in silicon to a microwave photon. Science 355, 156–158 (2017).
- Bruhat, L. E. et al. Circuit QED with a quantum-dot charge qubit dressed by Cooper pairs. Phys. Rev. B 98, 155313 (2018).
- Samkharadze, N. et al. Strong spin-photon coupling in silicon. Science 359, 1123–1127 (2018).
- Mi, X. et al. A coherent spin–photon interface in silicon. Nature 555, 599–603 (2018).
- Landig, A. J. et al. Coherent spin–photon coupling using a resonant exchange qubit. Nature 560, 179–184 (2018).
- Vandersypen, L. M. K. et al. Interfacing spin qubits in quantum dots and donors—hot, dense, and coherent. npj Quantum Information 3, 1–10 (2017).
- Borjans, F., Croot, X. G., Mi, X., Gullans, M. J. & Petta, J. R. Resonant microwave-mediated interactions between distant electron spins. Nature 577, 195–198 (2020).
- Scarlino, P. et al. Coherent microwave-photon-mediated coupling between a semiconductor and a superconducting qubit. Nature Communications 10, 3011 (2019).
- Landig, A. J. et al. Virtual-photon-mediated spin-qubit–transmon coupling. Nature Communications 10, 5037 (2019).
- van Woerkom, D. J. et al. Microwave Photon-Mediated Interactions between Semiconductor Qubits. Phys. Rev. X 8, 041018 (2018).
- Scarlino, P. et al. All-Microwave Control and Dispersive Readout of Gate-Defined Quantum Dot Qubits in Circuit Quantum Electrodynamics. Phys. Rev. Lett. 122, 206802 (2019).
- Scarlino, P. et al. In-situ Tuning of the Electric Dipole Strength of a Double Dot Charge Qubit: Charge Noise Protection and Ultra Strong Coupling. arXiv:2104.03045 [cond-mat] (2021).
- Lodari, M. et al. Low percolation density and charge noise with holes in germanium. arXiv:2007.06328 [cond-mat, physics:quant-ph] (2020).
- Forn-Díaz, P., Lamata, L., Rico, E., Kono, J. & Solano, E. Ultrastrong coupling regimes of light-matter interaction. Rev. Mod. Phys.91, 025005 (2019).
- Frisk Kockum, A., Miranowicz, A., De Liberato, S., Savasta, S. & Nori, F. Ultrastrong coupling between light and matter. Nature Reviews Physics 1, 19–40 (2019).
- Masluk, N. A., Pop, I. M., Kamal, A., Minev, Z. K. & Devoret, M. H. Microwave Characterization of Josephson Junction Arrays: Implementing a Low Loss Superinductance. Phys. Rev. Lett. 109, 137002 (2012).
- Niepce, D., Burnett, J. & Bylander, J. High Kinetic Inductance NbN Nanowire Superinductors. Phys. Rev. Applied 11, 044014 (2019).
- Shearrow, A. et al. Atomic layer deposition of titanium nitride for quantum circuits. Appl. Phys. Lett. 113, 212601 (2018).
- Grünhaupt, L. et al. Granular aluminium as a superconducting material for high-impedance quantum circuits. Nature Materials 18, 816–819 (2019).