Introduction
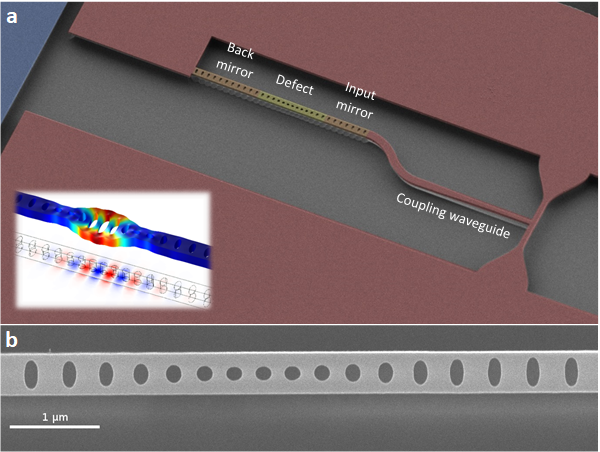
In this project we study quantum optomechanics using optomechanical crystals [1]. These are silicon nanobeams where a periodic array of holes creates both a phononic and photonic bandgaps. A local perturbation in the array creates allowed modes inside the bandgap. This leads to co-localized mechanical and optical modes that are dispersively coupled due to electrostrictive and geometric effects.
Due to their small size, the mechanical frequency of optomechanical crystals is in the GHz range, resulting in intrinsically lower phonon occupation than other typical oscillators of lower frequency. In fact, they can be prepared in the ground state – requisite for many quantum experiments – at millikelvin temperatures in a dilution refrigerator. However, as in many optomechanical systems, operation is limited by optical absorption heating. The plummeting thermal conductance of silicon at cryogenic temperatures combined with the vacuum environment of the refrigerator, result in poor thermalization to the cryogenic environment, and have limited experiments to the few photon level [2] or pulsed operation [3–6].
We chose to work with a 3He buffer gas cryostat, where the sample is kept at 0.5-5.0 K in ambient vapor above condensed 3He. The buffer gas enables efficient thermalization and allows us to probe the mechanical oscillator at relatively high powers. Reaching low phonon levels and even the ground state is possible using optomechanical sideband cooling [7]. This enables us to perform many interesting quantum optomechanics experiments using this promising system.
Motional Sideband Asymmetry in the Presence of Thermal Effects
One quantum signature of mechanical motion is different emission and absorption rates from the environment – inherent in the fact that in the ground state, an oscillator can absorb, but not emit, energy. The ratio of absorption to emission is (n + 1) / n where n is the mean thermal occupation of the oscillator. These two asymmetric rates are associated with the negative and positive frequency components of mechanical motion, and the effect is known as motional sideband asymmetry.
Motional sideband asymmetry thus enables self-calibrated temperature measurement based on the laws of quantum mechanics, and in fact form the basis of fiber based temperature sensors. They have also in observed in systems such as trapped ions.
In quantum optomechanics, motional sideband asymmetry has been observed in various setups [8–11]. It is known that the asymmetry can be corrupted by classical noise in the probe laser, masking the quantum effects. We have demonstrated another potential source of measurement error that manifests when additional proximate laser tones are applied. The ensuing oscillating optical field drives various optical nonlinearities, such as the photothermorefractive effect, Kerr effect etc., and modifies the effective scattering rate. The true quantum asymmetry is only revealed when such nonlinearities are mitigated, for example by operating beyond their bandwidth.
We have subsequently demonstrated optomechanical sideband cooling, self-calibrated using motional sideband asymmetry, down to 1.5 quanta.
Backaction-Evasion Measurements
Ultraprecise measurement of the position of a mechanical object has recently enabled the direct observation of gravitational waves [12], and also plays a key role in force sensing applications [13]. Continuous monitoring of the position is, however, fundamentally limited by the Heisenberg uncertainty relation – the measuring probe acts back on the measured system’s momentum, altering its motion [14,15] termed quantum backaction (QBA). In a mechanical oscillator, an optimal balance between imprecision and backaction leads to a sensitivity equal to the oscillator’s zero-point motion. Decades ago, research on this quantum revealed that it can be circumvented by monitoring only a single quadrature of the motion (e.g. amplitude), which leads to shunting of all backaction to the complementary quadrature (e.g. phase) [14,15].
Quantum backaction-evading measurements have been recently demonstrated in an electromechanical oscillator coupled to a resonant microwave circuit at mK temperatures [16], and subsequently utilized in the generation of squeezed states of mechanical motion [17,18].
We have demonstrated backaction evasion measurement in the optical domain. By using two probe lasers, tuned to the upper and lower mechanical sidebands, we couple exclusively to a single quadrature. Using sideband asymmetry we can calibrate the oscillator occupation and gauge the amount of backaction that is evaded, which is more than 10% of the oscillator motion.
This demonstration is an important step in surpassing the quantum limit of continuous position measurement, and paves the way towards generation of mechanical squeezed states in the optical domain.
References
[1] M. Eichenfield, J. Chan, R. M. Camacho, K. J. Vahala, and O. Painter, Nature 462, 78 (2009).
[2] S. M. Meenehan, J. D. Cohen, S. Gröblacher, J. T. Hill, A. H. Safavi-Naeini, M. Aspelmeyer, and O. Painter, Phys. Rev. A 90, 011803 (2014).
[3] S. M. Meenehan, J. D. Cohen, G. S. MacCabe, F. Marsili, M. D. Shaw, and O. Painter, Phys. Rev. X 5, 041002 (2015).
[4] R. Riedinger, S. Hong, R. A. Norte, J. A. Slater, J. Shang, A. G. Krause, V. Anant, M. Aspelmeyer, and S. Gröblacher, Nature 530, 313 (2016).
[5] R. Riedinger, A. Wallucks, I. Marinković, C. Löschnauer, M. Aspelmeyer, S. Hong, and S. Gröblacher, Nature 556, 473 (2018).
[6] S. Hong, R. Riedinger, I. Marinković, A. Wallucks, S. G. Hofer, R. A. Norte, M. Aspelmeyer, and S. Gröblacher, Science 358, 203 (2017).
[7] A. Schliesser, R. Rivière, G. Anetsberger, O. Arcizet, and T. J. Kippenberg, Nat Phys 4, 415 (2008).
[8] A. H. Safavi-Naeini, J. Chan, J. T. Hill, T. P. M. Alegre, A. Krause, and O. Painter, Phys. Rev. Lett. 108, 033602 (2012).
[9] A. J. Weinstein, C. U. Lei, E. E. Wollman, J. Suh, A. Metelmann, A. A. Clerk, and K. C. Schwab, Phys. Rev. X 4, 041003 (2014).
[10] T. P. Purdy, P.-L. Yu, N. S. Kampel, R. W. Peterson, K. Cicak, R. W. Simmonds, and C. A. Regal, Phys. Rev. A 92, 031802 (2015).
[11] M. Underwood, D. Mason, D. Lee, H. Xu, L. Jiang, A. B. Shkarin, K. Børkje, S. M. Girvin, and J. G. E. Harris, Phys. Rev. A 92, 061801 (2015).
[12] LIGO Scientific Collaboration and Virgo Collaboration, B. P. Abbott et al., Phys. Rev. Lett. 116, 061102 (2016).
[13] D. Rugar, R. Budakian, H. J. Mamin, and B. W. Chui, Nature 430, 329 (2004).
[14] C. M. Caves, K. S. Thorne, R. W. P. Drever, V. D. Sandberg, and M. Zimmermann, Rev. Mod. Phys. 52, 341 (1980).
[15] V. B. Braginsky, Y. I. Vorontsov, and K. S. Thorne, Science 209, 547 (1980).
[16] J. Suh, A. J. Weinstein, C. U. Lei, E. E. Wollman, S. K. Steinke, P. Meystre, A. A. Clerk, and K. C. Schwab, Science 344, 1262 (2014).
[17] F. Lecocq, J. B. Clark, R. W. Simmonds, J. Aumentado, and J. D. Teufel, Phys. Rev. X 5, 041037 (2015).
[18] E. E. Wollman, C. U. Lei, A. J. Weinstein, J. Suh, A. Kronwald, F. Marquardt, A. A. Clerk, and K. C. Schwab, Science 349, 952 (2015).