Introduction
Crystalline Microresonators [1–5] confine light on a circular trajectory (a so called whispering gallery mode) within the resonator material. The confinement results from the refractive index contrast of the dielectric resonator material with its surrounding environment (air or vacuum). The low intrinsic material absorption of the crystalline magnesium fluoride (MgF2) enables record long light storage time on the order of several microseconds. During this time the light completes more than 100.000 roundtrips inside the resonator, with a roundtrip length of several millimeters. The long light storage times are often quantified in terms of Quality-factor (Q-factor). The ultra-high quality factors achievable in crystalline micro-resonators routinely exceed a billion (109), which translates into a resonance width below 100 kHz. Light can be coupled efficiently into and out of the resonator using tapered fibers [3].
We are exploring a new application where optical solitons are used in the creation of optical frequency combs in these passive microresonators [6]. At high enough intensities nonlinear interactions between the light and the microresonator occur. As a result, a single frequency of light (coherent pump drive) can generate a pair of other frequencies as a result of the intensity dependent refractive index (Kerr effect) of MgF2 [7]. If the process cascades, many new frequencies are created. However, these interactions not always a well-defined relation between all generated frequencies [8] and in that case, the resulting optical frequency combs are not useful for many applications.
Solitons offer a solution to this problem. They consist of light pulses circulating in the cavity while retaining their shape. The dispersion of such cavity solitons is balanced by the material nonlinearity, but in addition their dissipation is balanced by the coherent driving of the cavity. This double balance effect allows cavity solitons to circulate indefinitely inside the resonator. The solitons created are in the form of ultrashort optical pulses of ~ 100 fs in duration which are stable in time [9]. Mathematically, they are described by a generalized driven, dissipative and detuned nonlinear Schrödinger equation: the Lugiato–Lefever equation [10]. The small roundtrip time of the soliton pulse means that the cavity outputs a train of optical pulses with a very high rate (> 10 GHz) and give rise to an optical frequency comb with wide line spacing, a regime that is not available to standard mode-locked lasers. Such Kerr frequency combs could be integrated in a very small package would enable many new applications.
We are exploring the dynamics of these dissipative Kerr solitons (DKS) in order to open new possibilities for applications of Kerr frequency combs. Due to the high Q properties of the crystalline microresonators, this platform is promising for low noise applications, as well as a great testbed to study the nonlinear dynamics of soliton.

Figure1: MgF2 crystal with two axial symmetric protrusions forming optical whispering gallery mode resonators.
Soliton dynamics: Breathing a natural instability …
Under certain operating conditions, the double balance effect is degraded and the soliton is destabilized and begins to oscillate – phenomenon called breathing – before collapsing and vanishing, owing to a tipping point in the equilibriums of the system. This type of instability is characteristic of non-linear dynamical systems and has been also observed in the dynamics of lasers near threshold, and even the evolution of species populations (Lotka-Volterra prey-predator model) or in the climate. In all these cases, early warning signs, such as the slowing of the oscillations, helps to some extent to predict a critical transition of the system (such as the extinction of a species).
The advantage of the optical system is that the time scales are very fast and a large number of realizations can be studied. We improved the control methods of the optical system allowing experiments to be carried out under well-defined parameters. Soliton breathing could be induced deterministically and the spatio-temporal dynamics directly observed. The study experimentally validates the predictions of numerical models, notably on the critical slowing down of the system and its evolution towards chaos.
As the soliton is more and more unstable, the amplitude of the oscillations increases and their frequency reduces, while the oscillation pattern becomes more and more incoherent and complex. The study also demonstrated that several solitons can interact and synchronize their oscillations.
These observations provide experimental validation of non-linear optical models in the unstable case. The methods developed by the scientists also provide a range of diagnoses to prevent these solitons instabilities and ensure a stable operation of the frequency combs.
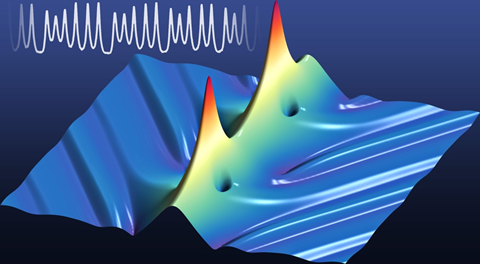
Figure 2: E. Lucas, M. Karpov, H. Guo, M. L. Gorodetsky & T. J. Kippenberg. Breathing dissipative solitons in optical microresonators. Nature Communications 8, 736 (2017).
… Or induced instability
Microresonators are often multimode, which means that they can guide light waves in more than one spatial pattern in the transverse direction and with different velocities in the propagation direction. In such cases, energy exchange between the soliton in one mode and the optical waveform in another can occur, which leads to the soliton breathing. This new regime is called a dynamic inter-mode breather soliton, and it can occur in configurations where dissipative Kerr solitons are normally stable. This was validated both in experiments and numerical simulations. An out-of-phase power oscillation in between the two modes was observed, indicating the energy exchange between the soliton and another waveform in the microresonator.
Compared to other regimes, inter-mode breather solitons reveal a novel type of instability in microresonator-based frequency combs, which highlights rich nonlinear dynamics of dissipative temporal structures in multi-mode microresonators, but should be avoided in applications.
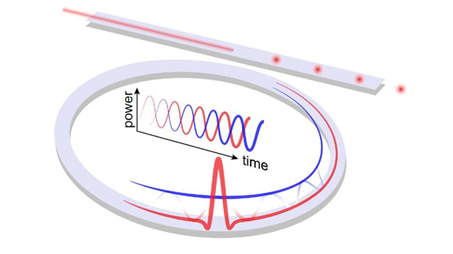
Figure3: H. Guo, E. Lucas, M. H. P. Pfeiffer, M. Karpov, M. Anderson, J. Liu, M. Geiselmann, J. D. Jost, T. J. Kippenberg. Intermode Breather Solitons in Optical Microresonators. Physical Review X 7, 041055, 06 December 2017. DOI: 10.1103/PhysRevX.7.041055
Spatial multiplexing for multiple combs generation
Spatial multiplexing is widely used in optical telecommunication to accommodate multiple wavelengths within spatially distinct fiber modes. Crystalline resonators support a large number of spatial modes, several of which can support soliton formation. We spatially multiplex DKSs in different mode families of the same resonator, in order to generate dual comb in both co- or counter-propagating configurations. We then combine these two schemes to generate three combs simultaneously. The soliton combs have a high degree of mutual coherence, which is desirable for many dual and triple comb schemes used in spectroscopy.
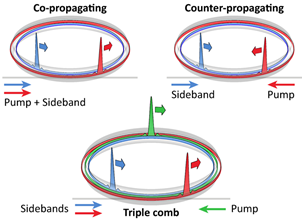
Figure4: Schematic representation of the DKS multiplexing in a single microresonator form : Lucas, E. et al. Spatial multiplexing of soliton microcombs. (2018), arXiv 1804.03706
Low Noise microwaves generation
The photodetection of the stable optical pulse train generated with mode-locked lasers is known to produce remarkably low phase noise RF carriers. We make use of DKS in microresonators to extend this capability in the microwave regime (> 10 GHz) and study the fundamental noise processes in DKS generation.
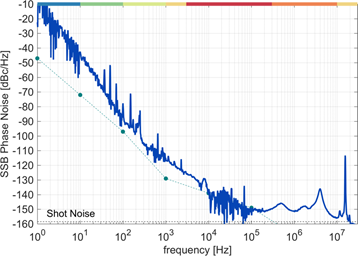
Figure5: Phase noise of a 14 GHz tone generated via photodetection of a DKS pulse train. The dotted line indicate the device noise floor, accounting for the number of cross-correlations.
References
[1] Braginsky, V. B., Gorodetsky, M. L. & Ilchenko, V. S. Quality-factor and nonlinear properties of optical whispering-gallery modes. Phys. Lett. A 137, 393–397 (1989).
[2] Grudinin, I. et al. Ultra high Q crystalline microcavities. Opt. Commun. 265, 33–38 (2006).
[3] Hofer, J., Schliesser, A. & Kippenberg, T. J. Cavity optomechanics with ultrahigh-Q crystalline microresonators. Phys. Reveiw A 82, 31804 (2010).
[4] Liang, W. et al. Generation of near-infrared frequency combs from a MgF2 whispering gallery mode resonator. Opt. Lett. 36, 2290–2292 (2011).
[5] Wang, C. Y. et al. Mid-infrared optical frequency combs at 2.5 μm based on crystalline microresonators. Nat. Commun. 4, 1345 (2013).
[6] S. T. Cundiff and J. Ye, Colloquium: Femtosecond optical frequency combs, Rev. Mod. Phys. 75, 325 (2003)
[7] P. Del’Haye, et al. Optical frequency comb generation from a monolithic microresonator. Nature 450, 1214-1217 (2007).
[8] T. Herr et al., Universal formation dynamics and noise of Kerr-frequency combs in microresonators. Nature Photonics 6, 480-487 (2012).
[9] T. Herr et al. Temporal solitons in optical microresonators. Nat. Photon. 8, 145–152 (2013).
[10] Lugiato, L. A. & Lefever, R. Spatial Dissipative Structures in Passive Optical Systems. Phys. Rev. Lett. 58, 2209–2211 (1987).