Contact: Julien Fageot
Levels: Master semester project, or Master thesis
Sections: IC, EE, SMA
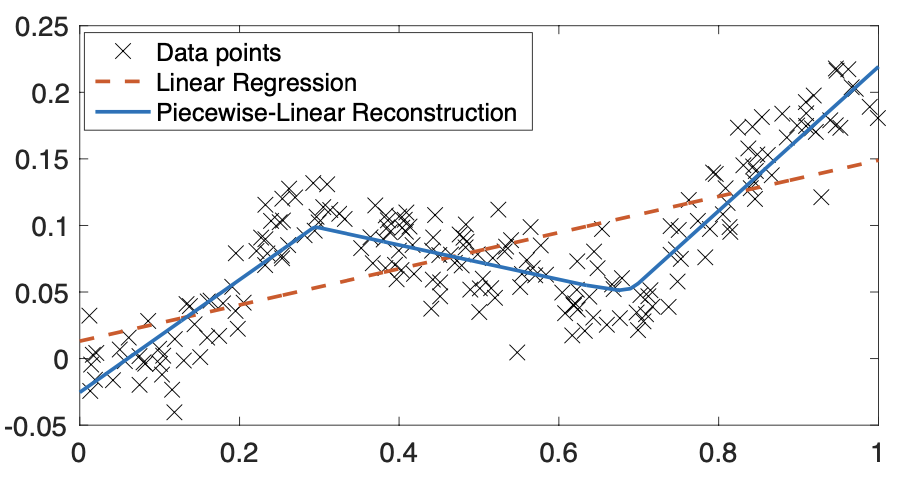
Recent works have investigated the possibility of recovering continuous-domain signals from their discrete observations using sparsity-promoting variational methods. The resulting interpolation problem is then cast as a functional sparse inverse problem. In this project, we focus on piecewise-linear continuous-domain reconstruction, which is achieved by regularising the inverse problem with the total-variation norm of the second derivative of the signal. Such reconstruction combines the advantage of simplicity and efficiency (for instance, deep neural networks based on ReLU activation functions actually perform piecewise-linear representations of the data) and allows for a sparse and adaptive signal representation.
The underlying optimization task has been recently studied in detail and an elegant and very efficient algorithm able to reach the sparsest piecewise-linear continuous-domain representation of the signal has been proposed. The goal of the project is to build on this breakthrough result and to perform an innovative statistical analysis of the functional and sparse reconstruction method. By relying on various probabilistic models, ranging from sparse (Poisson processes) to smooth (Gaussian processes) models, one main objective will be to quantify the statistical properties and performances of the proposed algorithm.
The project will include both theoretical and computational aspects that can be adapted to the student’s scientific interests. Being at ease with statistics, optimization, functional analysis, and advanced learning topics is expected.
Reference:
[1] Thomas Debarre, Quentin Denoyelle, Michael Unser, Julien Fageot, Sparsest Continuous Piecewise-Linear Representation of Data (2020). arXiv.