Movie: Nonadiabatic quantum dynamics of a 3-state, 4-dimensional model of pyrazine induced by a sequence of ultrashort pump and probe laser pulses
Ultrafast time-resolved spectroscopy
One of our interests is the development of efficient methods for computing ultrafast time-resolved spectra (Wehrle et al 2011,Sulc and Vanicek 2012,Sulc et al 2013,Zambrano et al 2013,33]. The figure shows a time-resolved stimulated emission spectrum of NCO computed with the Cellular Dephasing Representation (CDR) using a single (!) semiclassical trajectory (Sulc and Vanicek 2012):
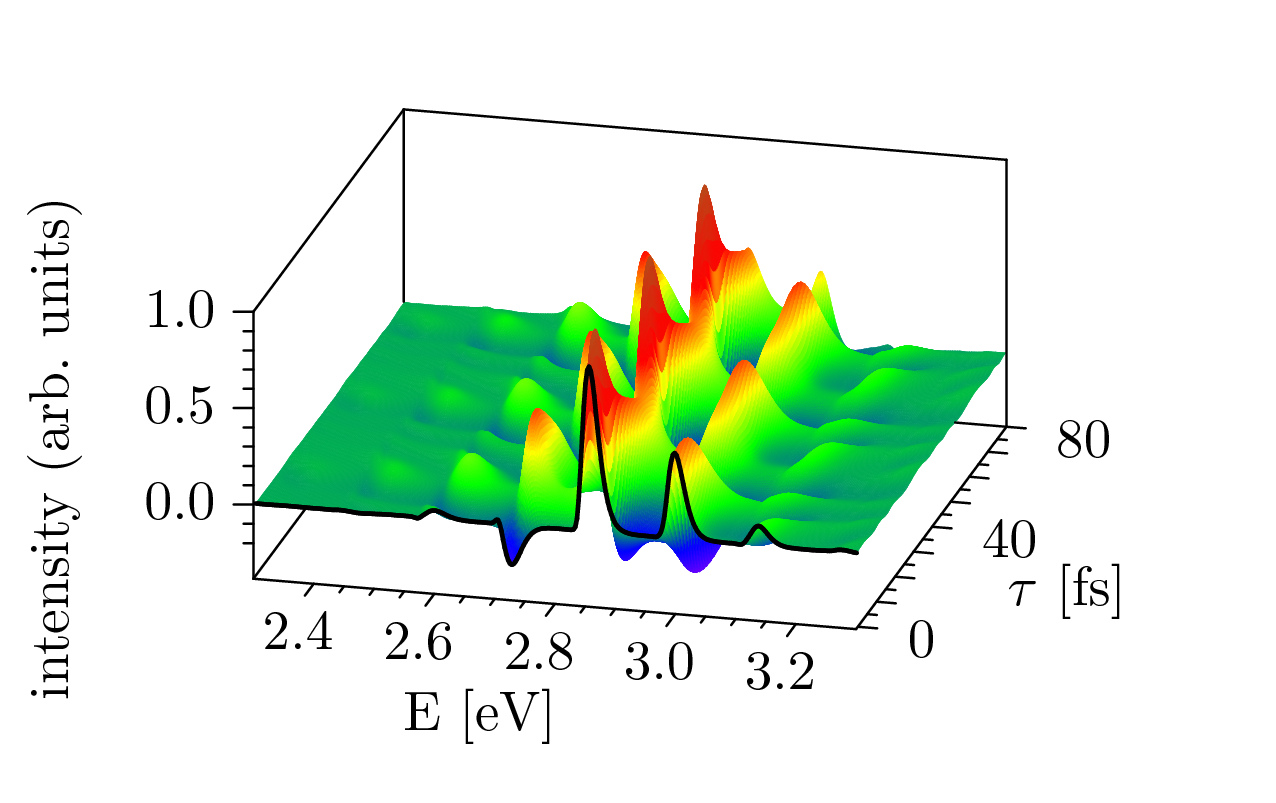 |
The CDR can be formalized using the inverse Weierstrass transformation, providing optimal choices of the sampling weight and width of Gaussian cells (Zambrano et al 2013). Additionally, the accuracy of this approximation can be improved with an amplitude correction derived from the phase-space propagator (Zambrano et al 2013).
On the other hand, starting from an exact Gaussian basis method, it is possible to derive the DR together with ten other methods for computing time-resolved spectra with intermediate accuracy and efficiency. These methods include the Gaussian DR, an exact generalization of the DR, in which trajectories are replaced by communicating frozen Gaussian basis functions evolving classically with an average Hamiltonian (Sulc et. al 2013).
“On-the-fly” ab initio quantum and semiclassical dynamics
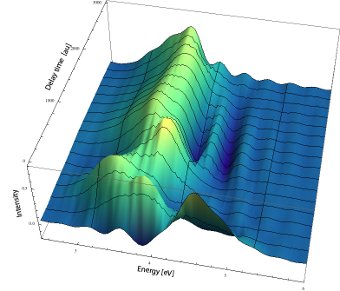
Recent advances in computer capabilities have made it possible to combine accurate quantum dynamics methods with “on-the-fly” computed ab initio electronic structure. In our group we are interested in developing on-the-fly ab initio semiclassical dynamics methods (Zimmermann and Vanicek 2012,33), particularly for applications in ultrafast spectroscopy. The figure below shows an on-the-fly ab initio time-resolved stimulated emission of azulene [33]:
 |
Nonadiabatic dynamics
Transitions between Born-Oppenheimer potential energy surfaces due to nonadiabatic and spin-orbit couplings play an important role in quantum molecular dynamics. In our group, we have designed a rigorous measure of the “nonadiabaticity” as well as an efficient semiclassical approximation to evaluate it (the so-called Multiple-Surface Dephasing Representation, MSDR) (Zimmermann and Vanicek 2010,Zimmermann and Vanicek 2012a). In the process we have also derived the locally mean field dynamics (LMFD) for the density matrix (Zimmermann and Vanicek 2012a). The figure below shows a snapshot of an “on-the-fly” ab initio nonadiabatic semiclassical dynamics of formaldimine. Different colors of hydrogen atoms designate the electronic surfaces on which the given trajectories run (Zimmermann and Vanicek 2012b):
Efficient evaluation of accuracy of molecular quantum dynamics using dephasing representation
Ab initio methods for electronic structure of molecules have reached a satisfactory accuracy for calculation of static properties, but remain too expensive for quantum dynamical calculations. We have proposed an efficient semiclassical method for evaluating the accuracy of a lower level quantum dynamics, as compared to a higher level quantum dynamics, without having to perform any quantum dynamics. The method is based on dephasing representation of quantum fidelity and its feasibility was demonstrated on the photodissociation dynamics of CO2.
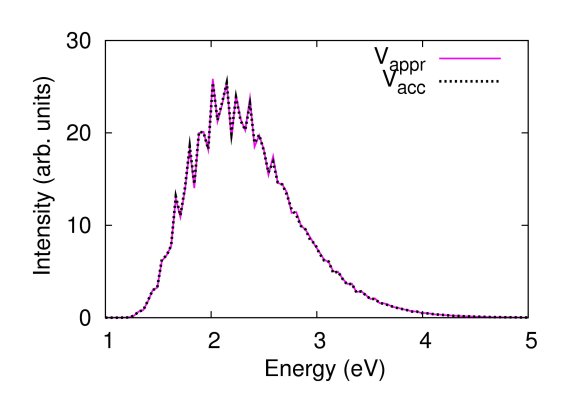
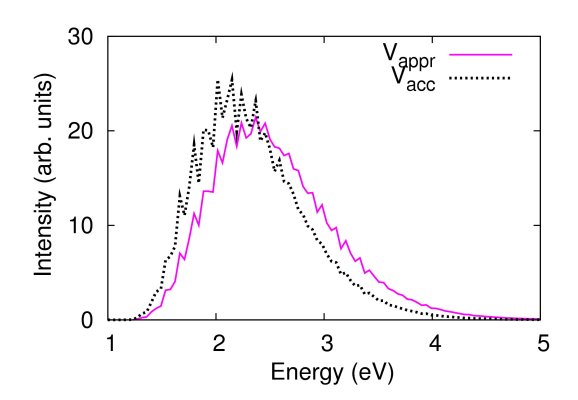
The figures below compare photodissociation spectra of CO2 computed by using two slightly different potential energy surfaces. In the first case (left figure), where the dissociation energy of the CO bond is perturbed by 0.02 eV, the spectra are very similar. In the second case (right figure), where the CO bond length is perturbed by 0.02 a.u., they are quite different. The contribution of our method described in Refs. [15,18] is that we can predict the accuracy/inaccuracy of the approximate spectrum very efficiently, without having to compute the more accurate spectrum.
For details, see: B. Li, C. Mollica, and J. Vanicek: “Efficient evaluation of accuracy of molecular quantum dynamics using dephasing representation,” Communication in J. Chem. Phys. (2009).
The method was combined with ab initio electronic structure calculations in Zimmermann et al 2010.