
Figure 2. Dew droplets on spider web, an example of RP instability in nature; source:[1]
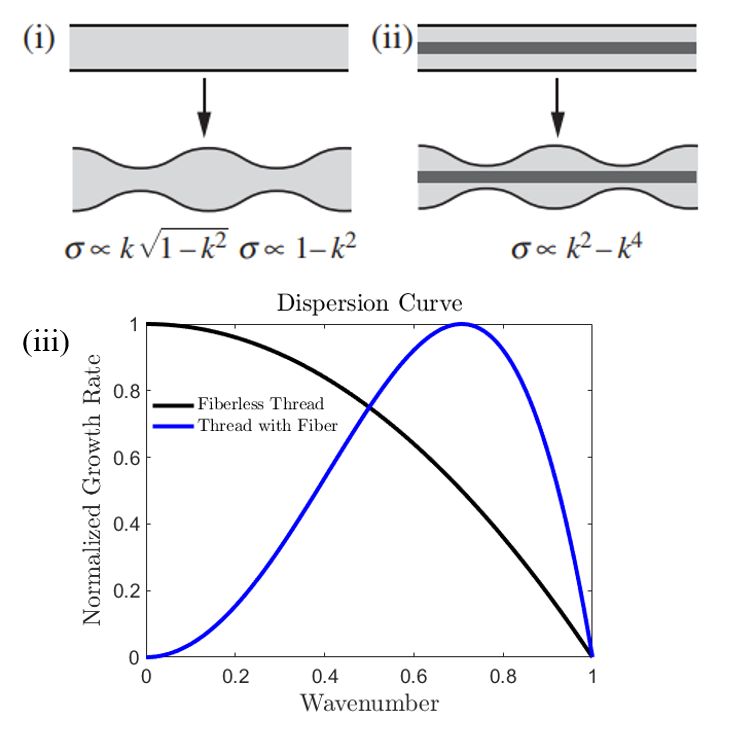
Figure 1. Instability modes: (i) Liquid thread; (ii) Liquid thread along a long fiber; source:[2] (iii) Dispersion curve
Project type: Master project
Project description:
Destabilization of cylindrical threads/jets into spherical droplets under the effect of surface tension is a well-known classical problem in Fluid Mechanics, known as Rayleigh-Plateau instability. Many aspects of this instability have been studied in the literature. It is known that by increasing the dominance of viscous dissipation, the outcome of destabilized jet varies from a set of well-distinguished monodispersed droplets, at low and intermediate viscosity, to a state where droplets of different sizes are formed, at high viscosity. Droplet size is predicted accurately by the linear stability analysis only in the former case. In the latter viscous case, introducing a solid fiber coaxial to the liquid thread enables to retrieve again the formation of a well distinguished monodispersed set of beads.
In this project, we will restrain to the highly viscous limit, and investigate the transition of the instability characteristics from a pure liquid thread to a liquid thread with a fiber along its axis. The purpose will be to precisely characterize the transition from a random droplet size selection (happening for a pure liquid jet) to a precise bead size selection (around a fiber). Implementing a regular distribution of equidistant solid fibers on the axis of the liquid thread, this transition will be investigated numerically. A theoretical analysis will also be carried out, in order to rationalize this transition from a shear-dominated viscous dissipation (long fiber case) to an extensional flow dissipation (no fiber case).
Finally, the student will also help to design future experiments illustrating his/her theoretical and numerical predictions.
Numerical Skills: FreeFem++ & MATLAB (linear stability analysis), COMSOL (Non-linear analysis)
Key words: Rayleigh-Plateau instability, extensional flow, linear stability analysis
Supervisors: Shahab Eghbali
References:
[1] https://www.pickpik.com/dew-drops-droplets-water-nature-pattern-macro-145798
[2] Gallaire, F. and Brun, P.T., 2017. Fluid dynamic instabilities: theory and application to pattern forming in complex media. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 375(2093), p.20160155.