Droplet flow in microchannels
The study of micro scale flows is motivated by the idea to build integrated circuits of micro channels for medical or chemo-/bio-analytical assays. These devices exist already for some applications like amplification of DNA.
Advantages of these micro assays are among others the need for very little material, high concentration, faster mixing by diffusion and integration of micro sensors. Some techniques have been developed to control these micro flows. The approach followed in this research favors the use of micro droplets with a volume of nano to pico liters. Using droplets as micro containers and transport vehicles allows the parallel screening of several substances exposed to several conditions or reagents. Crucial however is the control and prediction of the flow.
We follow a theoretical and numerical approach towards the understanding of droplet behavior in flow fields including surface tension, surface tension gradients and surfactants.
Changing from macro scale to micro scale flow has an important impact on the physics. As some physical aspects are neglected on a macro scale changing the scale means to incorporate new aspects by neglecting others. That means including surface tension and omitting non linear inertial terms. In this multiphase context one deals with a free boundary between the two immiscible fluids. Taking benefit of the large aspect ratio of microchannels, which are much thinner than wide, we use depth-averaged Stokes equations to run simulations based on boundary elements fulfilling the specific requirements of these multiphase micro flows. The adsorption/desorbtion dynamics of surfactants are to be added in future.
Simulation of Complex Microfluidic Circuits (SimCoMiCs)
This project is funded by the European Research Council. ![]()
The focus of SimCoMiCs is to develop tools that bridge the gap between complex microfluidic circuits in experimental research and numerical simulations. The channel geometry requires in principle prohibitive three-dimensional simulations, except in some simplified flows.
In our approach we decomposed the real problem into two different planes. One plane corresponds to the plane that is visible under a microscope, characterized by being very polymorph in geometrical and parametric configuration (as seen in the animations below).
The second plane, perpendicular to the first has a dominant impact due to its smaller size in flat channels. The velocity gradients and curvature are thus higher and produce a dominant contribution to the flow, however there is only little variance in channels of constant height.
With this idea in mind, we have developed Ulambator a simulation tool based on a boundary element technique that aims at representing the physics of micro scale flows but remains at the same time simple and efficient enough to run computations lasting minutes to a few hours on a desktop computer.
An open-source version of Ulambator is available here for user who wish to try it on their own cases.
A collection of results:
I. Relaxation of droplets
A deformed droplet in the absence of flow will relax to a circular shape when it is only confined by top and bottom walls and not by lateral walls from the side. The reason is that the surface tension pulls on the interface so the droplet deforms to the state that has the lowest interfacial area.
Droplet relaxiation times can be used to probe material properties of the droplet like surface tension or viscosity. When experimental data of the relaxing droplet interface is sampled the geometry information is noisy and could match it to a family of given shape in order to compress the information.
We figured out that there is a common curve, an attractor to whcih deformed droplets relax. This attractor state is not an ellipse, which on might assumed because ellipses are a family of curves that differ by their radius and excentricity and that include the circle as the zero excentricity limit. As a starting point we simulated different ellipses and observed their relaxation.
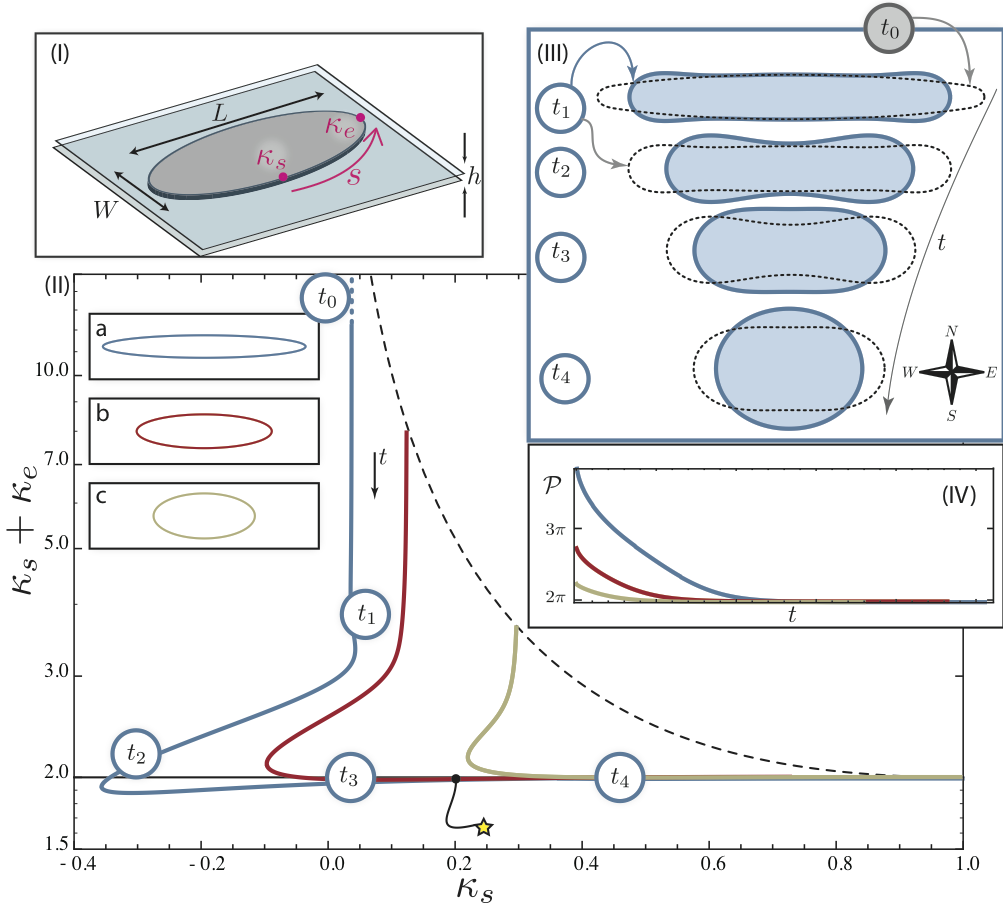
The figure above displays the sum of a southern and eastern curvature on an elliptic droplet plotted against the southern curvature. The convention is that the east (and west) points are the maximal curved points on the interface and south (and north) are the least curved points. The dashed line represents different ellipses and the coloured lines are the states that an inilitally elliptic droplet undergoes when turning into a circle.
All curvature trajectories instantaneously deviate from the curve of ellipses (dashed line). Instead they tend rapidly to a state where the sum of the two curvatures is twice the equilibrium curvature. We have derived an equation for this common curve and named it the kappa-2 ovals.
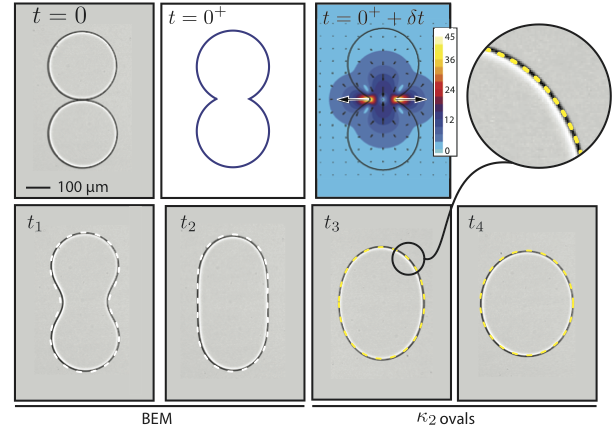
An experimental study strengthend our proposition to use the kappa-2 ovals as a attractor curve. Two droplets that merge in a microchannel although moving slowly (at low Capillary number) neatly follow the relaxation curve predicted by Ulambator using the Boundary Element Method and in their final stage they conform well with the kappa-2 oval. The experiments on a microfluidic chip in PDMS where filmed with a high-speed camera at 15000 images per second.
II. Capturing of droplets
Microfluidic devices allow for rather repeatable processes because random processes due to turbulence are suppressed at low Reynolds number. However flow control becomes challenging because of the small size. Apart from active actuators a promissing strategy is passive control. A recent development by Dangla et al. in the group of Charles Baroud at LadHyX in Paris, France, uses indentations in microchannels to capture and buffer droplets.
The indentations are perpendicular to the flow plane and therefore not genuinely captured in our 2D approach. However since we model the dominant influences from the thin direction (Direction of Dominance) we can introduce the surface tension effects due to the presence of the hole to our solver.
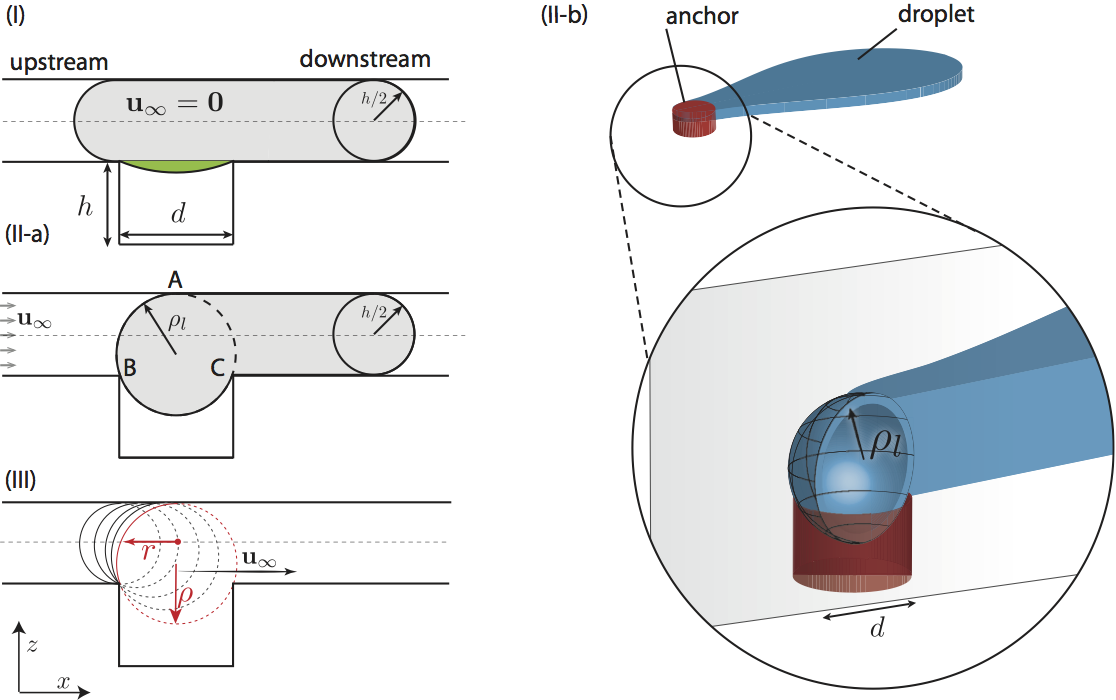
The droplet can minimize its surface area when it attaches to the indentation, which corresponds to a smaller pressure jump over the interface at the cap region that is immersed in the indentation. By deriving a simple geometric model we can prescribe the pressure jump in the Direction of Dominance around the droplet.
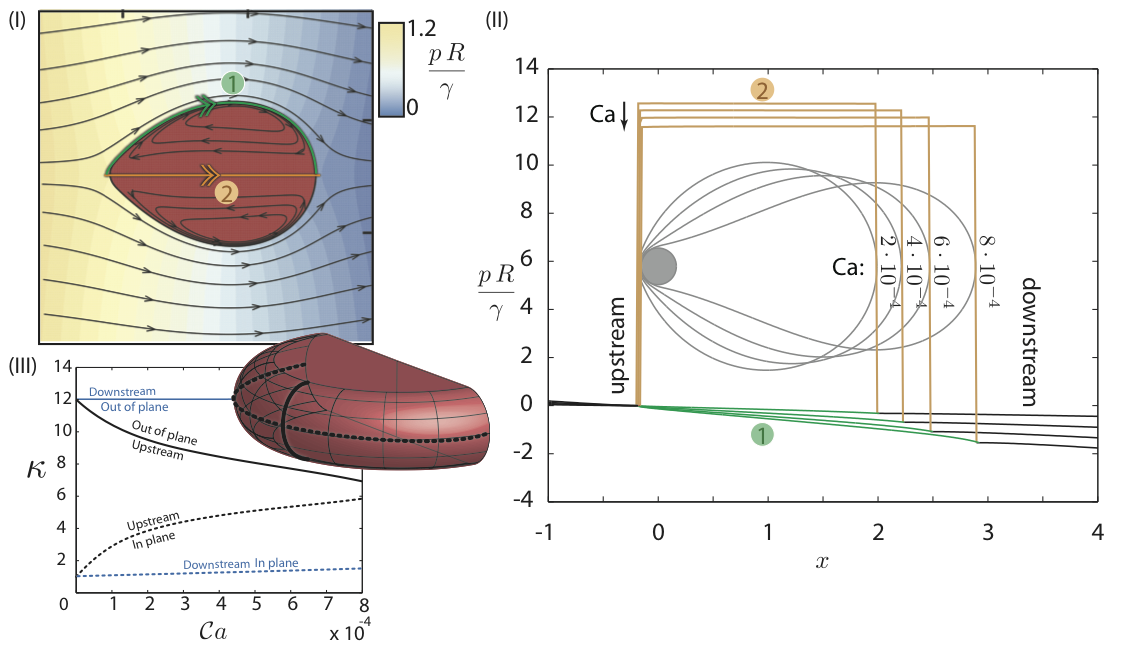
The simulation shows that the lower pressure jump in the front region minus the pressure jump in the rear region leads to a force that can resist the viscous force and therefore anchors the droplet to a certain threshold.

When comparing the deformation of the droplet on the anchor (shown above) and the critical threshold above which droplets detach (not shown) a good agreement is obtained.
References:
Generic path for droplet relaxation in microfluidic channels, Physical Review E, vol. 88, num. 4, 2013.
A numerical study of droplet trapping in microfluidic devices, Physics of Fluids, vol. 26, num. 3, p. 032002, 2014.
A Matlab code that calculates the velocity of a droplet with dynamic film formation in a Hele-Shaw cell. The hydrodynamic forces are calculated with the depth-averaged Brinkman equation and the curvature modification are calculated according to the Landau-Levich-Bretherton law.
Usage: U/V = dropvel(Ca, lambda, R/H)
U = droplet velocity
V = velocity in the far field
Ca = viscosity outer fluid*V/surface tension
lambda = viscosity droplet/viscosity outer fluid
R = radius of droplet
H = height Hele-Shaw cell