Type: Semester/Master project
Orbital sloshing is a method to gently mix the liquid content of a container by its displacement along a circular trajectory at a constant angular speed, that is often used in biological and chemical industrial applications as an alternative to stirred tanks. Drawing upon the experimental observation of Bouvard et al. [1], our main objective consists of predicting the wave-induced toroidal and poloidal mean flows. This is a challenging task that hinges on the subtle modelling of the boundary layer region in the neighborhood of the moving contact line, whose dynamics holds pivotal significance in governing the mean flow generation in the system but whose analytical modelling appears particularly challenging [2].
From a numerical modeling point of view, difficulties arise due to the highly multiscale nature of the problem (length scales extending from the macroscopic to the molecular sizes). We will use Basilisk [3], an open-source software for the solution of partial differential equations, to simulate the dynamic contact lines using various models [4] on arbitrarily shaped surfaces. An initial validation on simple two-dimensional cases, comparing the results to existing experiments and numerical studies, will be followed by an investigation of the sloshing dynamics (Figure 1.).
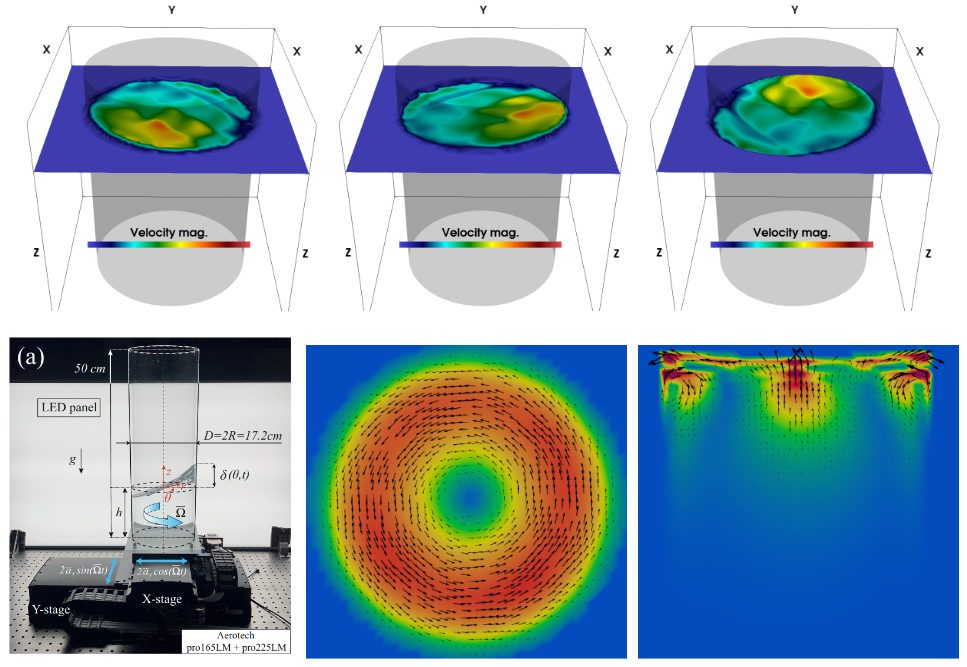
[1] Bouvard et al., Phys. Rev. Fluids 2 (2017).
[2] A. Marcotte, F. Gallaire & A. Bongarzone. Phys. Rev. F. (2023).
[3] http://basilisk.fr/
[4] Fullana, T. PhD Thesis, Sorbonne University (2022).
Supervisors: Tomas Fullana & François Gallaire