FNSNF Projects

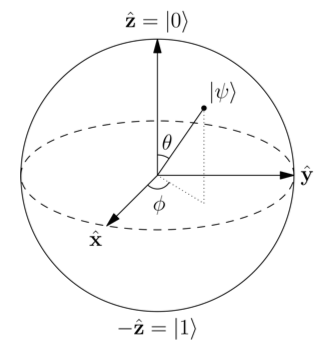
Current project:

Deep Optimisation

Swiss National Science Foundation (200021_205011)

Thanks to neural networks (NNs), faster computation, and massive datasets, machine learning (ML) is under increasing pressure to provide automated solutions to even harder real-world tasks with beyond human performance with ever faster response times due to potentially huge technological and societal benefits. Unsurprisingly, the NN learning formulations present a fundamental challenge to the back-end learning algorithms despite their scalability, in particular due to the existence traps in the non-convex optimization landscape, such as saddle points, that can prevent algorithms to obtain “good” solutions.
Our recent research has demonstrated that the non-convex optimization dogma is false by showing that scalable stochastic optimization algorithms can avoid traps and rapidly obtain locally optimal solutions. Coupled with the progress in representation learning, such as over-parameterized neural networks, such local solutions can be globally optimal. Unfortunately, we have also proved that the central min- max optimization problems in ML, such as generative adversarial networks (GANs) and distributionally robust ML, contain spurious attractors that do not include any stationary points of the original learning formulation. Indeed, algorithms are subject to a grander challenge, including unavoidable convergence failures, which explain the stagnation in their progress despite the impressive earlier demonstrations.
As a result, the proposed Deep Optimization Project (DOPE) will confront this grand challenge in ML by building unified optimization and representation foundations in how we capture functions via non-linear representations, how we set-up our learning objectives that govern our fundamental goals, and how we optimize these goals to obtain numerical solutions in scalable fashion. We contend that optimization problems, such as non-convex non-concave min-max, cannot be studied in isolation from the context they are formulated. By exploiting the properties of the representations, we can invoke structures to obtain favorable convergence or actively discover which types of external oracles are necessary to guarantee convergence to “good” solutions.

Past Projects:

Theory and Methods for Accurate and Scalable Learning Machines

Swiss National Science Foundation (407540-167319/1)

This project rethinks the design of the next generation of online learning systems to enable the technology to deal with Big Data-sized data sets, such as MOOCs. The project also seeks to validate the quality of our learning results using statistical theory. Based on this new machine learning framework, we focus on implementing an individualised online learning system to enhance students’ learning experience by automatically exploring their learning style and skills. Moreover, we will study the decision problems in the design of such individualised systems and develop an appropriate (Bayesian) optimisation framework for their automation.

Large-Scale Sparse Bayesian Modeling, Inference, and Design

Team: Volkan Cevher [PI], Andreas Krause @ ETHZ [co-PI], Jarvis Haupt @ UMN [co-PI]

   Dates: 2013 – 2016 [PhD students: Marwa El Halabi, Josip Djolonga and Ilija Bogunovic]
Rasante Entwicklungen in der Sensortechnologie, der Robotik und der Signalverarbeitung versprechen neuartige Intelligente Informationssysteme (IIS), die in der Lage sind, grosse Mengen an vielfältigen mobilen oder stationären Sensoren zu koordinieren. Solche Systeme haben grosses Potential in Anwendungen wie der autonomen Umweltüberwachung, der medizinischen Bildgebung, dem automatischen Experiment-design etc. 
Auf dem Weg zur Entwicklung solcher Intelligenten Informationssysteme stellen sich mehrere zentrale Herausforderungen:
1) Die Datenflut, verursacht durch hochauflösende, hochfrequente Messungen neuartiger Sensoren, die in Echtzeit verarbeitet werden müssen ohne die Kommunikationsnetze dabei zu überlasten;
2) Die Notwendigkeit, komplexe, nichtlineare (nicht-konvexe und kombinatorische) Berechnungen durchzuführen, um aus dieser Datenflut Informationen zu extrahieren;
3) Der Umgang mit Unsicherheiten, verursacht durch verrauschte Daten, die in den Berechnungen eine zentrale Rolle spielen.
Dieses Projekt hat das Ziel, diese Herausforderungen geschlossen anzugehen, durch Zusammenführung dreier Schlüsselkonzepte: Sparsity (Dünnbesetzheit; kombinatorische Struktur in natürlich auftretenden Signalen); Submodularität (eine mathematische Eigenschaft kombinatorischer Probleme, die die Entwicklung effizienter Algorithmen ermöglicht) sowie Bayes’scher Inferenz (die robusten Umgang mit Unsicherheit erlaubt). Diese Konzepte wurden bisher weitgehend unabhängig voneinander untersucht. Wir sind davon überzeugt, dass Synergien zwischen diesen zentralen Konzepten von IIS nur in einem gemeinschaftlichen Ansatz entdeckt und nutzbar gemacht werden können. In diesem Projekt werden wir neuartige Algorithmen entwickeln, die diese Schlüsselkonzepte zusammenführen, sie theoretisch untersuchen und in verschiedenen Anwendungen im Bereich Umweltbeobachtung, medizinische Bildgebung sowie Bildverstehen einsetzen und evaluieren.

Scalable and Accurate Quantum Tomography

Swiss National Science Foundation (200021-146750)

Dates: 2013-2016 [PhD student: Yen-Huan Li]

In this project, we are concerned with optimized information extraction from quantum measurements. Our key contention is that while the ambient dimension is large in quantum tomography, the relevant state information therein resides in a much lower dimensional space due to physical nature of the quantum systems. We use this powerful observation to develop new theory and algorithms under a low-dimensional modeling for information extraction from low-dimensional or incomplete data.

Theory and methods for compressive sensing with graphical models [GM-CS]

Swiss National Science Foundation (200021-132620)
Dates: 2011-2013 [PhD student: Anastasios Kyrillidis]

Compressive sensing (CS) is an emerging alternative to Shannon/Nyquist sampling paradigm for simultaneous sensing and compression of signals having a sparse representation. By sparse representation, we mean the signal can be well approximated by a few nonzero coefficients in some basis. According to CS, the number of compressive measurements for stable recovery is proportional to the signal sparsity, rather than to its Fourier bandwidth. For this reason, CS permits revolutionary new sensing designs and algorithms for dimensionality reduction.

This project exploits probabilistic graphical models in CS as realistic signal models that can capture underlying, application dependent order of sparse coefficients, and as sampling matrices with information preserving properties that can be implemented in practical systems.