Les transformations de phase structurelles impliquent une phase parent et une phase fille, généralement liées par une relation d’orientation (RO) spécifique. Les transformations sont déclenchées par le refroidissement, la déformation, ou plus généralement en changeant une condition externe. Dans les alliages ferreux par exemple, Dans les alliages de fer par exemple, la phase parent austénitique cubique face centrée (cfc) est transformée par trempe en une phase fille martensitique cubique centrée (cc) ou tétragonale centrée (tc) avec une relation d’orientation proche de celle découverte par Kurdjumov et Sachs (KS) en 1930, comme illustré sur la figure 1. Dans les aciers à faible teneur en carbone, la transformation est presque terminée sans austénite parentale conservée. Les informations sur les grains parents antérieurs ne sont cependant pas perdues et peuvent être récupérées à partir des orientations des grains filles mesurées par diffraction à rétrodiffusion d’électrons (Electron Back-Scatter Diffraction ou EBSD) ou des techniques équivalentes. Ceci est important car les joints de grains parents contiennent souvent des impuretés qui peuvent avoir des effets importants sur les propriétés mécaniques.
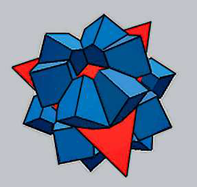
Fig. 1. Représentation géométrique en 3D des 24 variants cc (cubes bleus) dans la relation d’orientation de Kurdjumov-Sachs avec un cristal parent cfc (tétraedre rouge)
Un programme informatique est en cours de développement depuis 2006 afin de reconstruire les grains parents antérieurs à partir de cartes EBSD acquises sur des matériaux entièrement transformés [1,2]. Le programme est basé sur une analyse cristallographique rigoureuse des variantes d’orientation et de leurs désorientations spécifiques (opérateurs). Les variantes sont les cosets basés sur le sous-groupe de symétries qui sont communs aux cristaux parents et filles. Les opérateurs sont les doubles cosets basés sur le même sous-groupe. Leur nombre est donné par la formule de Lagrange et Burnside, respectivement. La structure algébrique formée par les variantes et leurs opérateurs est un groupoïde [3]. Les calculs des variantes et des opérateurs sont très rapides (quelques ms) et nécessitent juste la connaissance des groupes de points des phases parent et fille et la relation d’orientation [4]. Pour toute transformation structurelle, un tableau théorique de composition groupoïde peut être établi. Ce tableau est à valeurs multiples si seuls les opérateurs sont composés; et elle est monovalée lorsque les variantes formant les opérateurs sont prises en considération. Un exemple 2D est donné sur la figure 2.

Fig. 2. Illustration simple d’une structure groupoïde avec un exemple 2D. Le caré parent a une relation d’orientation avec les triangles filles. Comme le nombre de symétries communes est 2 (identité et symétrie miroir m), le nombre de variantes est 8 (nombre de symétries d’un carré) divisé par 2 = 4. Il y a 3 opérateurs (identité O0, rotation d’un quart de tour O1 , inversion O2). Leur composition est mutuelle si les variants qui forment les opérateurs ne sont pas pris en compte. Elle devient monovaluée lorsqu’une variante (ici la variante 1) est prise comme référence.
Les tableaux théoriques de composition des groupoïdes sont calculés une fois pour toutes pour les principales transformations structurelles, et ils peuvent être directement utilisés pour traiter les données expérimentales EBSD. Le programme de reconstruction utilise une approche de «nucléation/croissance» illustrée schématiquement sur la figure 3.
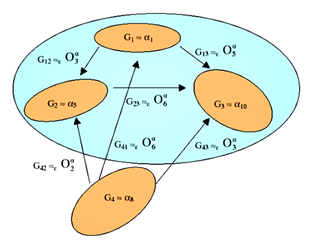
Fig. 3. Algorithme de nucléation/croissance utilisé pour reconstruire les grains parents. Trois grains fille voisins sont choisis; on vérifie que les désorientations entre eux sont proches des opérateurs théoriques avec un faible angle de tolérance et que les désorientations sont composées suivant le tableau de composition théorique. Si coché, les trois grains sont considérés comme un «noyau». Ensuite, les noyaux se développent suivant la même procédure mais avec un angle de tolérance plus grand.
La reconstruction fonctionne avec succès pour les grains austénitiques antérieurs dans les aciers martensitiques et bainitiques [1,2], comme le montre la figure 4, les grains bêta antérieurs dans les alliages de titane et de zirconium [2], et les grains cubiques parents dans la zircone monoclinique [5 ] etc.
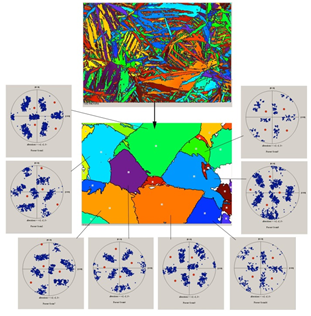
Fig. 4. Exemple de reconstruction des grains austénitiques antérieurs dans un acier bainitique. Remerciements pour la carte originale: Dr A.A. Shirzadi, Cambridge, Royaume-Uni.
La reconstruction offre également la possibilité de tracer des cartes de relation d’orientation (et pas seulement des orientations) dans les aciers martensitiques [6], comme illustré sur la Fig. 5, et aide l’utilisateur à quantifier la sélection des variants dans les aciers en colorant les groupes de variants (paquets cristallographiques dans les plans denses, paquets de direction denses, paquets Bain, groupes de plaques).
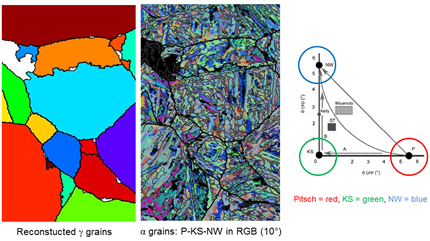
Fig. 5. Coloration RVB des relations d’orientation dans un acier martensitique. Grains austénitiques antérieurs reconstruits, avec les variantes cc colorées selon un code de coloration RVB: Rouge = RO Pitsch, Vert = RO KS et Bleu = Nishiyama-Wasserman.
Le programme peut être utilisé pour traiter le cas de maclages multiples dans des matériaux cfc afin de quantifier l’effet des traitements thermomécaniques sur les fractions de macles (ingénierie des joints de grains) [7], comme illustré succinctement sur la figure 6.
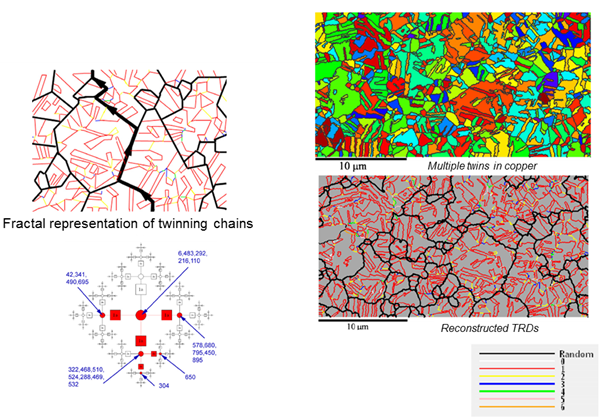
Fig. 6. Domaines liés par maclage (Twin Related Domains ou TRD) dans les métaux cfc. Pendant les traitements de recuit, des macles Σ3 peuvent se former pendant la croissance des grains, et ces macles peuvent former des macles, qui peuvent former des macles, etc. Les assemblages de grains cfc liés par la chaîne de macles Σ3 sont appelés un domaine de maclage apparenté. Comme les joints de grains maclés Σ3 ont des propriétés spéciales (faible résistivité électrique, faibles taux de corrosion), il est souvent intéressant de relier les propriétés macroscopiques aux tailles des TRD. Le programme de reconstruction peut être utilisé pour effectuer le travail automatiquement. Les chaînes de maclage d’ordre élevé (jusqu’à l’ordre de 6 et plus) peuvent être identifiées dans les lignes d’interconnexion en cuivre.
Le programme est entièrement automatique, rapide et facile à utiliser, mais il souffre également de certaines limitations. Les matériaux hautement déformés sont difficiles à reconstruire; la texture parentale et la taille des grains sont bien rendues mais les limites parentales exactes sont mal définies et sont sensibles aux paramètres de reconstruction, comme illustré sur la Fig. 7. Un article indépendant examinant les avantages et les limites du programme de reconstruction peut être trouvé dans la réf. [8]. Le programme continue d’évoluer avec les commentaires des utilisateurs et les nouveaux besoins. Des programmes similaires sont également développés dans le monde entier en France, au Japon, aux États-Unis, en Inde, etc.

Fig. 7. Reconstruction des grains austénitiques parents dans un acier Eurofer déformé en tension le long de l’axe y à 1100 ° C jusqu’à la rupture et immédiatement trempé. Les limites parentales ne sont pas bien reconstruites (contours hirsutes) mais la texture parentale est bien rendue. Remerciements: Prof. Hugo Ricardo Zschommler Sandim, Université de São Paulo, Brésil.