Structural phase transformations imply a parent phase and a daughter phase, generally linked by a specific orientation relationship (OR). The transformations are triggered by cooling, deforming or more generally by changing an external condition. In iron alloys for example, the parent austenitic face-centered cubic (fcc) phase is transformed by quenching into a daughter martensitic body-centered cubic (bcc) or body-centered tetragonal (bct) phase with an OR close to the one discovered by Kurdjumov and Sachs (KS) in 1930, as illustrated in Fig. 1. In low carbon steels, the transformation is nearly complete with no retained parent austenite. The information on the prior parent grains is however not lost and can be retrieved from the orientations of the daughter grains measured by Electron Back Scatter Diffraction (EBSD) or equivalent techniques. This is important because the parent grain boundaries often contain impurities that can have significant effects on the mechanical properties.
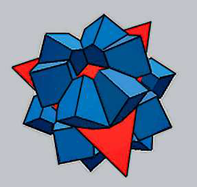
Fig. 1. 3D geometrical representation of the 24 bcc variants (blue cubes) in Kurdjumov-Sachs orientation relationship with a parent fcc crystal (red tetrahedron)
A computer program is being developed since 2006 in order to reconstruct the prior parent grains from EBSD maps acquired on fully transformed materials [1,2]. The program is based on a rigorous crystallographic analysis of the orientational variants and their specific misorientations (operators). The variants are the cosets based on the subgroup of symmetries that are common to the parent and daughter crystals. The operators are the double-cosets based on the same subgroup. Their number is given by Lagrange and Burnside formula, respectively. The algebraic structure formed by the variants and their operators is a groupoid [3]. The calculations of the variants and operators are very rapid (few ms) and just need the knowledge of the point groups of the parent and daughter phases and the orientation relationship [4]. For any structural transformation, a theoretical groupoid composition table can be established. This table is multivalued if only the operators are composed; and it is monovalued when the variants forming the operators are taken into consideration. A 2D example is given in Fig. 2.

Fig. 2. Simple illustration of a groupoid structure with 2D example. The parent square is in orientation relationship with the daughter triangles. As the number of common symmetries is 2 (identity and mirror symmetry mx), the number of variants is 8 (number of symmetries of a square) divided by 2 = 4. There are 3 operators (identity O0, rotation by a quarter turn O1, inversion O2). Their composition is mutivalued if the variants that form the operators are not considered. It becomes monovalued when a variant (here variant 1) is taken as a reference.
The theoretical groupoid composition tables are calculated for the main structural transformations once and for all, and they can directly be used to treat the experimental EBSD data. The reconstruction program uses a “nucleation/growth” approach schematically illustrated in Fig. 3.
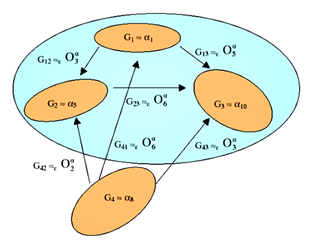
Fig. 3. Nucleation/growth algorithm used to reconstruct the parent grains. Three neighbor daughter grains are chosen; it is checked that the misorientations between them are close to theoretical operators with a low tolerance angle and that the misorientations are composed following the theoretical composition table. If checked, the three grains are considered as a “nucleus”.Then the nuclei grow following the same procedure but with a larger tolerance angle.
The reconstruction works successfully for the prior austenitic grains in martensitic and bainitic steels [1,2], as shown in Fig. 4, the prior beta grains in titanium and zirconium alloys [2], and the parent cubic grains in monoclinic zirconia [5] etc.
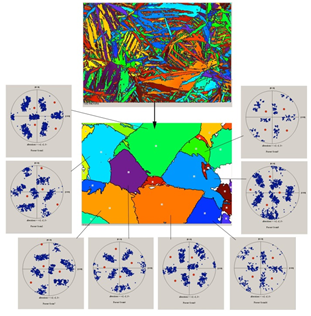
Fig. 4. Example of reconstruction of the prior austenitic grains in a bainitic steel. Acknowledgements for the original map: Dr. A.A. Shirzadi, Cambridge, UK.
It also offers the possibility to plot maps of orientation relationship (and not only orientations) in martensitic steels [6] , as illustrated in Fig. 5, and it helps the user to quantify variants selection in steels by coloring the variant groups (close-packed plane crystallographic packets, close-packed direction packets, Bain packets, plate groups).
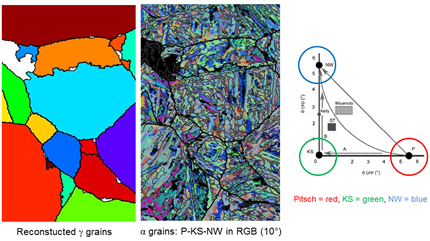
Fig. 5. RGB coloring of orientation relationships in a martensitic steel. Reconstructed prior austenitic grains, with the bcc variants colored according to a RGB coloring code : Red = Pitsch OR, Green = KS OR and Blue = Nishiyama-Wasserman.
The program can be used to treat the case of multiple twinning in fcc materials in order to quantify the effect of thermomechanical treatments on the twin fractions (grain boundary engineering) [7], as succinctly illustrated in Fig. 6.
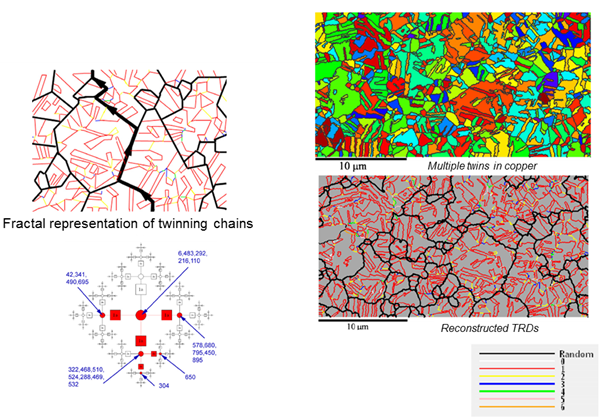
Fig. 6. Twin related domains (TRD) in fcc metals. During annealing treatments, Σ3 twins can be formed during the grain growth, and these twins can form twins, which can form twins etc. The assemblies of fcc grains linked by Σ3 twin chain is called a twin related domain. As Σ3 twin grain boundaries have special properties (low electrical resistivity, low corrosion rates), it is often interesting to link the macroscopic properties to the TRD sizes. The reconstruction program can be used to do the job automatically. High order twinning chains (up to order 6 and more) can be identified in copper interconnection lines.
The program is fully automatic, fast and easy to use, but it also suffers some limitations. Highly deformed materials are difficult to reconstruct; the parent texture and grain sizes are well rendered but the exact parent boundaries are badly defined and are sensitive to the reconstruction parameters, as illustrated in Fig. 7. An independent paper investigating the advantages and limitations of the reconstruction program can be found in ref. [8]. The program continues to evolve with the user’s comments and new needs. Similar programs are also developed world-wide in France, Japan, USA, India etc.

Fig. 7. Reconstruction of the parent austenitic grains in a Eurofer steel deformed in tension along the y-axis at 1100°C till rupture and immediately quenched. The parent boundaries are not well reconstructed (shaggy contours) but the parent texture is well rendered. Acknowledgement: Prof. Hugo Ricardo Zschommler Sandim, University of São Paulo, Brazil.
[8] S. Weyand, D. Britz, D. Rupp, F. Mücklich, Investigation of austenite evolution in low-steel by combining thermo-mechanical simulation and EBSD data, Mater. Perf. Charact. 4 (2015) 322-340.