Medical cyber-physical systems are a new trend of software controlled physical systems that are increasingly common in medical domains. These systems are becoming more and more popular in medical therapy. Medical service is more efficient and convenient for doctors and patients, while they offer the opportunities for medical experts and doctors in studying the treatments and in communicating with patients.
Therefore, patients can benefit from the automation of treatment process, which improve therapy effectiveness, lifestyle quality and reducing cost. However, with rapid developments in medical science and computer technology, medical cyberphysical systems are becoming more and more precise and complex, and more real-time reactions of the patient during treatment are sampled and analyzed. Due to the complexity of the systems and a low tolerance for faults in the medical environment, validation and verification of medical cyberphysical systems are crucial. Specifically, the challenges of verifying medical systems mainly come from timed and hybrid properties. Similarly to all cyber-physical systems, medical systems are mostly about the intersections of computations and physical actions. To create the mathematical models of the entire systems, formal methods that combine both discrete and continuous dynamics are required.
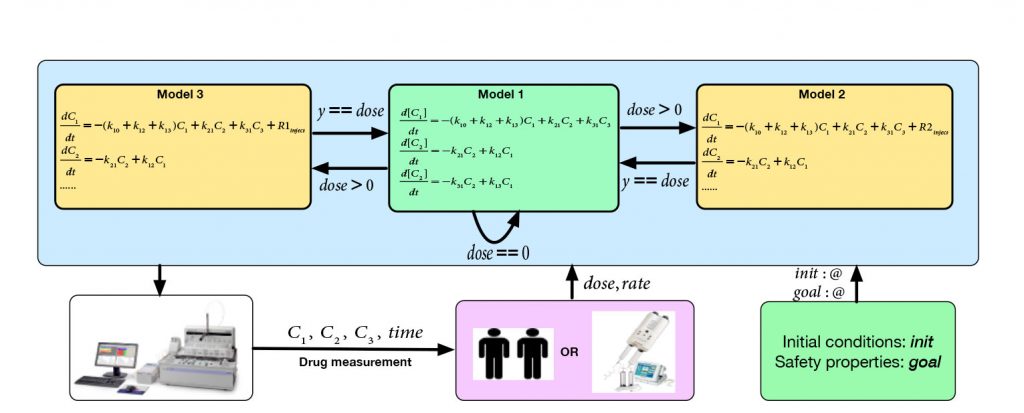
Formal methods have been widely used in checking the properties and reliabilities of hybrid systems, which are modeled using abstract mathematical representations. The main advantage of formal methods comes from the mathematical precision for reasoning the correctness of system models. Timed Automata plays a big role in modeling and verifying the timed systems. Particularly for medial systems such as drug administration system, such methods model the behavior of the system using formal representation by employing Timed Automata extended with Tasks(TAT). Tools such as UPPAAL and its extension TIMES have been successful in verifying cyber-physical systems in many domains.
To precisely model medical systems, a realistic drug response model has to be used. Various clinical studies show that responsiveness to the treatment with drugs depends on the concentration of the drug in the blood that depends on patients, drug dose, and intake time interval. Pharmacokinetics (PK) is a branch of pharmacology focused on studying the drug disposition in the human body. For many drugs, the concentration in the blood of a patient is highly related to its effectives. Pharmacodynamics (PD) is the study of the biochemical and physiological effects of drugs on the body. Therapeutic Drug Monitoring (TDM) is the approach that unifies the PK-PD knowledge, which shows that drugs with explicit PK-PD relationships and a narrow therapeutic range may be easily under- or overdose. Hence, it is important to develop an approach that generates safety guidance for medical injection using a precise drug response model, such as the drug administration system. In addition, Area Under the Curve (AUC), as well as AUC in the baseline measurements (constrained AUC), are commonly used to assess the extent of exposure of a drug. Measuring these two metrics is very important in pharmacokinetics analysis.
Our project has addressed the following issues.
1. We have introduced a general model for medical injection system, which can be applied to both simulation and formal verification, using Satisfiability Modulo Theory (SMT) over Reals. The mathematical three-compartment pharmacokinetics model is used for drug response in the abstract timed model, which is one of the most precise pharmacokinetics models for simulating drug response.
2. The model is demonstrated that it can efficiently and precisely simulate the medical injection process. The model can formally prove(disprove) if the expected drug concentration-time objectives are reachable ewith given injection actions, and return sat/unsat by checking bounded δ-satisfiability.
3. The proposed model computes AUC and constrained AUC simultaneously during the verification or simulation process. For computing constrained AUC, we have introduced an algorithm based on proof of unsatisfiability of SMT over real numbers.