Contact between rough surfaces
A major challenge in contact mechanics stems from the multi-scale nature of phenomena occurring at the contact. Natural surfaces are made of a vast number of asperities over a wide range of length scales, which induces a much smaller contact area than the observable one.
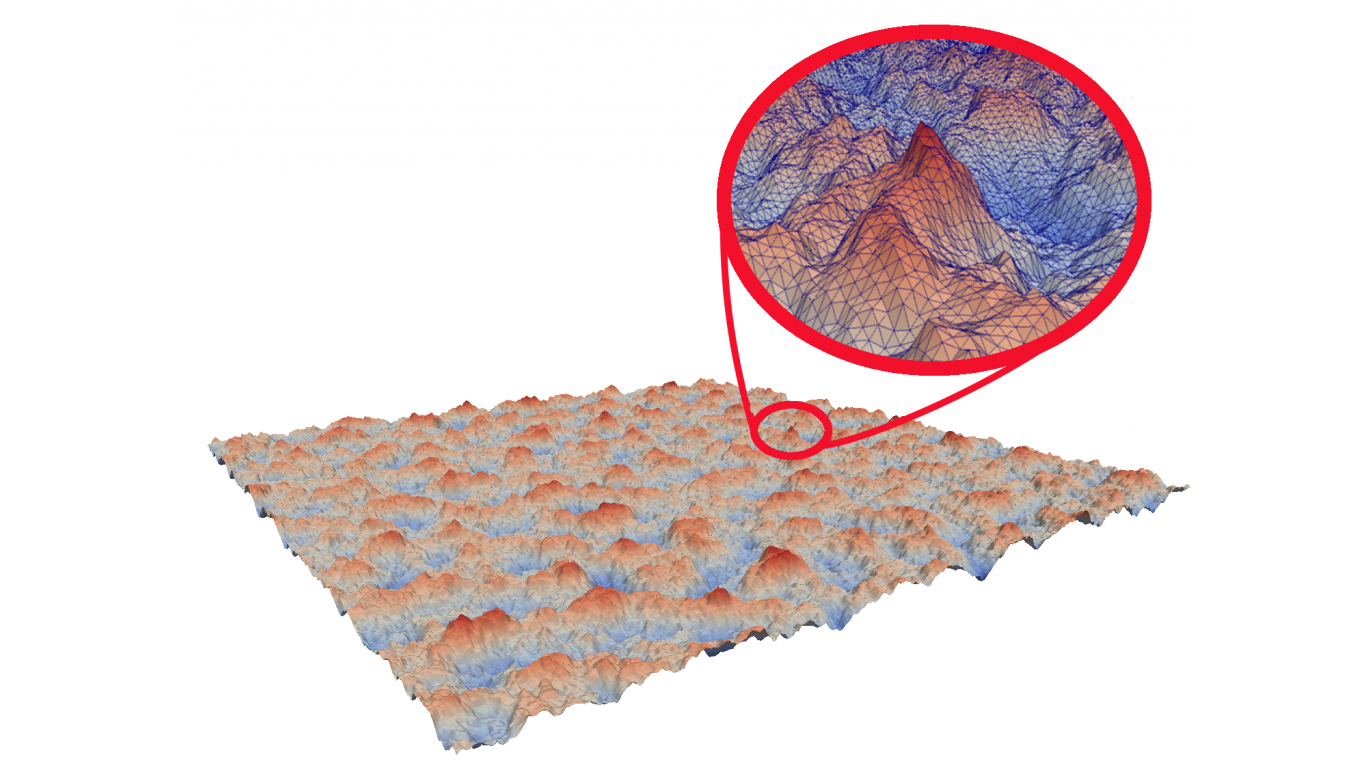
Rough surfaces are usually modeled as a Gaussian random field with a self-affine fractal-like structure. From a given rough surface, we can compute the solution of the contact problem using discretization methods such as Finite Element Method (FEM) or Boundary Element Method (BEM). In order to agglomerate sufficient statistical data, a lot of simulations have to be realized. Our research aims at developing new numerical techniques by casting the contact problem into a fully statistical framework, which will provide means to analyze statistical properties at lower costs. We collaborate with CSQI laboratory in EPFL to propose new efficient methods for the statistical analysis of contact quantities.
Elasto-plastic contact
When two metallic bodies are in contact, although the apparent pressure may be small, the local pressures, due to asperities entering in contact, are sufficient to cause plastic deformation of the materials. The consequences are irreversible deformations, residual stresses and hardening of the materials, which modifies the overall contact response. Therefore, pure elastic computations become irrelevant for the simulation of contact of metallic bodies.
We are investigating the effect of plasticity on the real contact area, the contact cluster distribution and the distribution of local pressures, using the Finite Element Method and the Boundary Element Method. However, the former breaks down for large surfaces, as the computational cost increases dramatically. We are therefore developing cutting edge numerical methods to solve the elasto-plastic contact problems in a high-performance environment.
Figure: Plastic volumes in rough surface contact
Cluster analysis in normal contact
When two solids with rough surfaces are in contact, the real contact area is only a fraction of the apparent zone of contact. This area plays a major role in various interface properties, like electric conductivity, heat conductivity, friction, etc. The contact area is decomposed into fractal patches, called contact clusters. Although the shape and number of these clusters is not important for properties such as electric conductivity, it plays a major role in the adhesive wear phenonmenon.
Our research in this topic consists of analysing the cluster distribution of a rough contact situation with varying load, and to show how the changes in distribution can affect the amount of wear happening between two solids. A video attach to this page shows how the contact clusters evolve with an increasing applied load, with clusters contributing to wear increasing in number and size.
Embed of video is only possible from Mediaspace, SwitchTube, Vimeo or Youtube
Adhesive normal contact
At the small scale, Van der Waals forces become non-negligible and adhesion need to be accounted for in simulations. One axis of our research consists in going from non-adhesive normal contact to adhesive normal contact. We have the capacity to study several adhesive pontetials and their consequences on the contact area and the distribution of contact clusters for different roughnesses.
Contact clusters with increasing normal load. Black corresponds to positive elastic pressure, white corresponds to negative elastic pressure and grey corresponds to zero pressure. We observe that adhesion takes place around contact patchs and connects them.