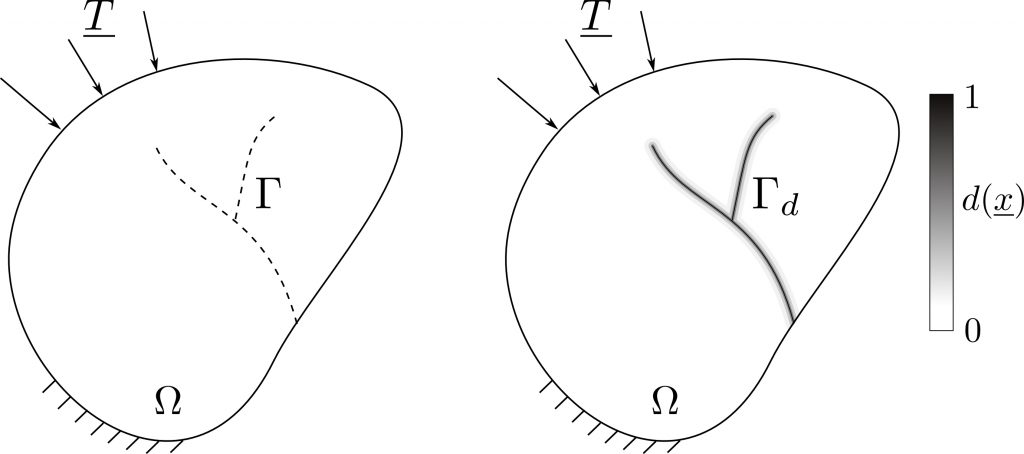
Context
For safety reasons, for instance in civil engineering, it is important to be able to predict the damage encountered by a structure after an accidental event. At LSMS, a strong focus is on dynamic loadings, such as impacts or explosions. For a reinforced concrete structure, the consequences are in general the development of a crack network, which can possibly lead to the ruin of the structure, but also for example to the loss of impermeability of confinement wall.
Two levels of prediction are then necessary. At the fine scale, we want to describe explicitly the cracks, from their initiation to their propagation and coalescence. Discrete models are used in this case, or finite elements coupled with the cohesive elements approach. The disadvantage of these methods, especially when high strain rates are considered, is that a fine spatial discretization is needed to reproduce the complex cracks patterns obtained (including merging, branching and instabilities). For computational cost reasons, it is not possible then to lead a computation at the scale of a structure. In that case, we rather use continuum models, such as damage models, where the cracks are not reproduced but considered through a variable that describe the degradation of the elastic properties.
Modeling explicitly the cracks enables to understand the local mechanisms of failure and calibrate the macroscopic damage models. In particular, the damage evolution law parameters can be fitted, and especially the strain rate effects. Indeed, if the strain rate increases, materials exhibit a higher strength in tension, which is generally assumed to be the consequence of the coalescence of multiple cracks. In quasi-static, the breakdown usually comes from the propagation of a unique macro-crack. Discrete models allow to reproduce these different phenomena, while they are considered phenomenologically in a continuum damage model.
On the other hand, macroscopic models can be useful to provide to the discrete modeling more precise loading conditions, since the real loading (impact for instance) and the global structural mechanisms (global bending, shear cone) can be reproduced.
Modeling of macro crack branching with continuum damage model
The macro crack branching in brittle materials is an unstable dynamic phenomenon which occurs when a single crack achieves a critical speed. The understanding of this phenomenon could lead to the design of energy-absorbing materials due to a correlation between the fracture toughness and the number of branches. The knowledge on the crack macro mechanisms could also improve the process of hydraulic fracturing. However, the branching mechanism is only partially understood. A possible way to understand this phenomenon are numerical tools. At LSMS, different continuum damage models are used to model the crack branching phenomenon.
Integral-type non local damage model
It is known that continuum damage model are ill-posed and lead to a localization of the damage in an arbitrary small volume, which translates into a strong mesh dependency as regards numerical implementation. Regularization techniques are then necessary to prevent spurious damage localization. The integral-type non-local model aims at defining a non-local measure of strains by performing a weighted average of the local strain values over a small volume around the current point. These models are able to reproduce complex crack patterns without mesh dependency.

Variational phase-field model
In the “phase-field” approach the crack topology is represented by a continuous field varying from 0 (sound material) to 1 (fully cracked material) across an internal length scale l 0 . It may be seen as a mathematical regularization of the variational approach to fracture developed by Francfort and Marigo in 1998 and is also strongly related to gradient damage models where the phase-field variable can be interpreted as the local level of damage inside the material. The main advantage of this type of method is that it does not require any a priori knowledge of the crack path or topology, modeling therefore very naturally nucleation, merging or branching phenomena. This technique is also used to get further insights of crack propagation in heterogeneous media.

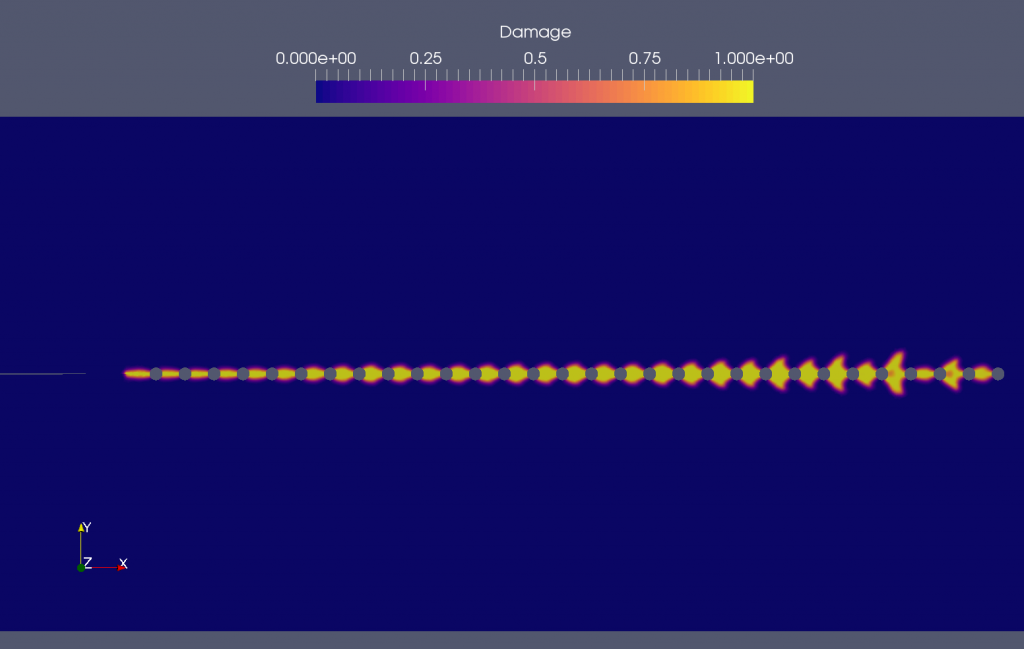
Figure 4 : Crack propagation through a perforated plate