Earthquakes can be devastating, both in terms of human and material damage. Although their existence has been known since the dawn of time, the physics of earthquakes is still poorly understood. Natural faults and earthquake characteristics are known to follow scaling power-law. The origin of this phenomenon has strong implications on the physical mechanisms driving slip events. However, it is not yet clear. The emergence of complexity can be related to the disorder of the system. Understanding if the observed complexity comes from the inherent complexity of the frictional motion or the system’s complexity is essential to better understand – and one day eventually predict – earthquakes. It has been shown numerically with a simple system without any disorder that resulting slip events follow a power-law distribution for the small events – like natural slip events – and a log-normal distribution for the larger ones. This project aims to study how adding disorder in this simple system will influence the transition between the power-law and the log-normal distribution of slip events. To do so, the student will use a finite element software developed in the lab (Akantu).
Supervisors:
Ferry Roxane Mathilde Suzanne, Jean-François Molinari

The interaction of soft solids with rigid surfaces during collision presents an interesting problem in mechanics with fundamental significance for biological soft tissues and soft robotics. Similarly to traditional fluid droplet impacts, soft solids exhibit unique behaviors when colliding with rigid surfaces, such as the formation of an annular contact region and the trapping of air between the surfaces.
This project will investigate the dynamics of soft solids impacting rigid surfaces, focusing specifically on the influence of surface topography. The final goal is to deepen the understanding of these interactions under controlled, quasi-static conditions.
The project will involve formulating and implementing a 2D finite difference numerical scheme in Python to simulate the problem, allowing for precise control over geometry and material properties. The student will use basic knowledge of linear elasticity, fluid mechanics and numerical methods.
Supervisors:
Jacopo Bilotto, Joaquin Garcia-Suarez, Jean-François Molinari

Granular materials play a critical role in civil, chemical, and mechanical engineering, influencing sectors such as food processing, pharmaceuticals, soil mechanics, and mixing technologies. The Discrete Element Method (DEM) is a powerful tool for simulating the behavior of particle systems by applying Newton’s laws of motion and friction. However, one significant limitation of DEM is its ability to accurately model materials that undergo large deformations.
To address this challenge, a recent reduced-order model, developed by Professor Mollon, offers an innovative approach to extend traditional DEM codes into the deformable regime. This project aims to evaluate the feasibility and stability of this novel method.
The student will implement the model using Python, leveraging the Taichi and NumPy libraries to efficiently code the method and test various interaction laws. Depending on the student’s interests, the project can be tailored to focus on either high-performance GPU computing or the mechanics of specific test cases.
Supervisors:
Jacopo Bilotto, Jean-François Molinari
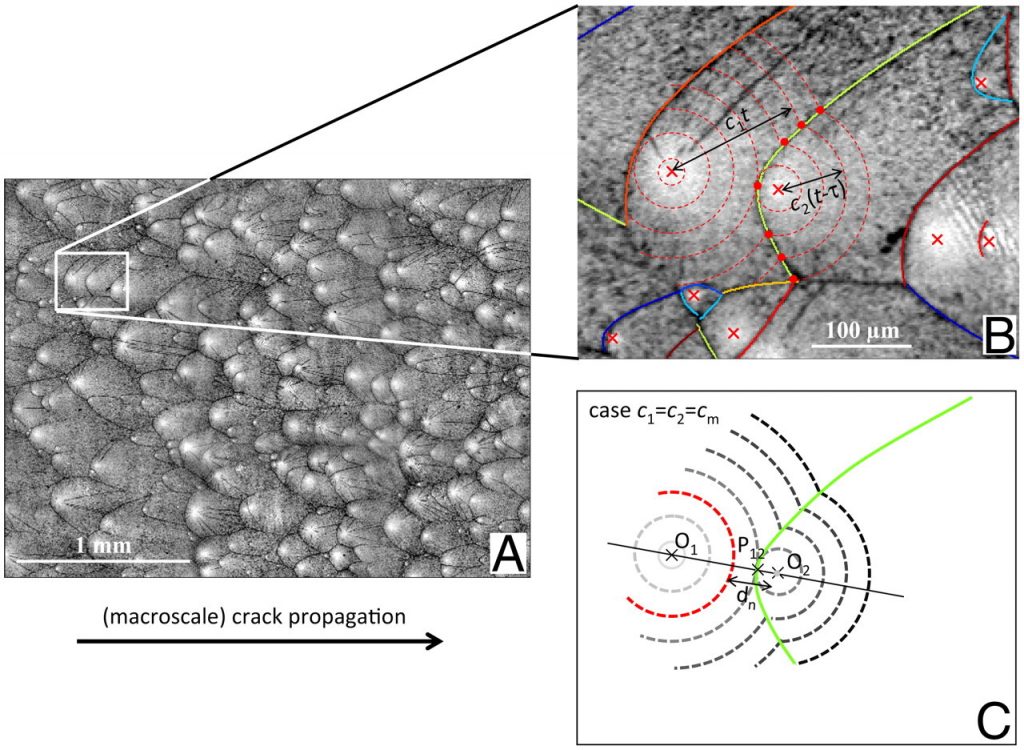
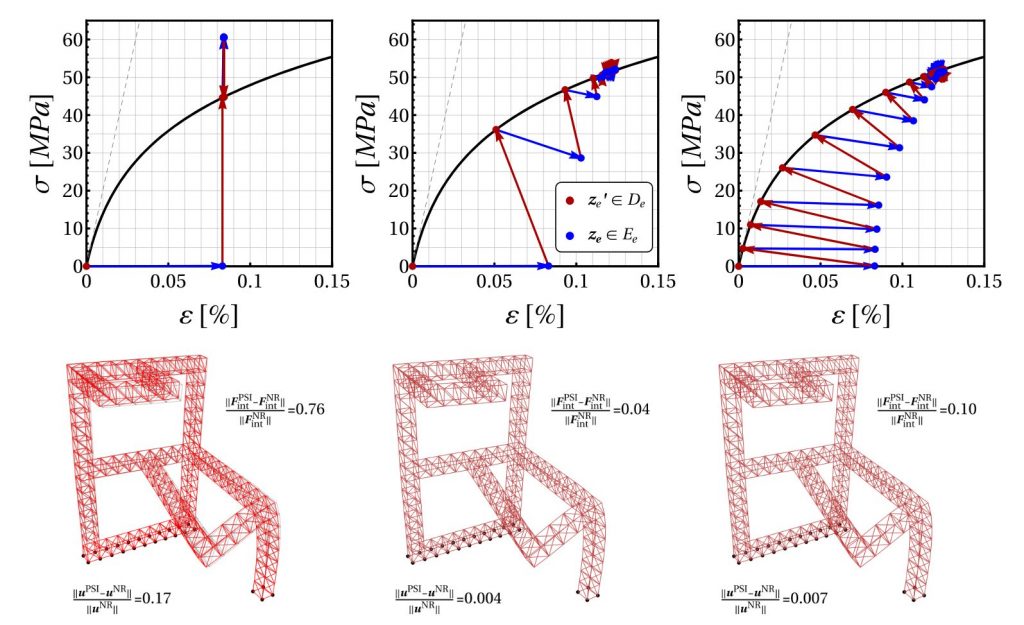
Extreme loads on solids lead to the formation of a multitude of cracks that propagate, branch and coalesce to form fragments. This process is called dynamic fragmentation. This process is of importance in many domains of engineering, where it is fundamental to predict the outcome of high velocity impacts or explosions. Often, one would like to extract statistics such as fragment size distribution. This project will feature experiments on object breaking into pieces to extract experimental statistics on fragments. The student will then use a finite element software (Akantu) to simulate crack propagation using different methods such as phase-field modelling of fracture or cohesive elements. The statistics obtained numerically will be compared to the experimental ones to highlight the advantage and limitations of the different simulation methods.
Supervisors:
Thibault Ghesquière-Diérickx, Jean-François Molinari

A study conducted on postmortem mode I fracture surfaces in polymethyl methacrylate (PMMA) found that, when the crack reaches a certain velocity, comet patterns are observed on the surface. They are the result of a complex rupture dynamic where the main crack propagates by nucleation, growth, and coalescence of microcracks ahead of the main front. Exploring models that incorporate interfaces containing inherent defects nucleated ahead of the main front can provide valuable insights into the mechanics of this fracture process.
The student will use an open-source Spectral Boundary Interface Model, cRacklet, and attempts to reproduce this complex fracture process using rate-dependent cohesive laws. This research project is an opportunity for the student to gain an understanding of fracture mechanics, as well as sharpening their skills in numerical methods and programming.