Introduction
Machine learning is one of the hottest scientific topics of the last decade. Neural networks are part of this field. They originated in the neurosciences and signal processing and have benefited from the enormous advances in computer science and the huge amounts of data that have been collected for various scientific problems over the last decades. Today, they are used in a wide range of topics to solve black-box problems, this means predicting the output of a system for a given input without knowing its internal workings. In our daily life, it is now widely used for translation purposes or as a working assistant with Large Language Models such as ChatGPT.
It is expected that the number of parameters required to make those model work will exceed the trillion mark as of 2025. These large models require an enormous amount of computing power for both training and inference. This pushes Moore’s law to its limit and has a huge environmental impact, as the number of parameter increasess exponentially and with it the number of GPU needed. This consumes a lot of energy and requires a lot of materials for production. Our goal is to involve physical systems in AI to perform calculations in a new way in order to solve this issue.
How it works
Waves naturally perform some elaborated computations such as integration, derivation [4] or classification in a passive way [1, 2]. To do this, it is necessary to control the propagation of the waves very precisely, which can be achieved for example with a specially structured propagating medium [2]. Also, a random scattering medium output can depend non-linearly on its input, given the high dimensionality of the output, it is possible to find underlying abstract parameters in the output to perform classification [5]. One of the main advantages is that waves with a small wavelength and a high bandwidth, e.g. in the optical range, the number of degrees of freedom (d.o.f.) can be as high as 10 trillion using a combination of spatial and spectral d.o.f. In addition, the speed of optical phenomena is higher than the speed of current processors which theoretically enables a higher processing power [3].
The main challenges in using such analog computing systems as neural-like networks are low scalability and training in terms of energy efficiency and compatibility. To train such analog neural networks on a large scale, numerous methods are currently being explored. Each method comes with its own trade-offs, and thus far, none has matched the scalability and performance of the backpropagation algorithm prevalent in deep learning today [6]. Nonetheless, this is evolving rapidly, and an expanding array of training techniques hints at how physical neural networks could eventually be harnessed to develop both more efficient implementations of current-scale AI models and to enable unprecedented-scale models.
What we are working on
In this race for ever more computing power, hardware and software are developing hand-in hand, inspiring and hindering one another. At LWE, we are trying to develop both new training algorithms and new experimental setups to demonstrate and develop the potential of wave physics in this adventure.
On the software side, the goal is to shift from “in-silico training” to “physical training” in order to minimize the digital computation during training and indeed enhance the power efficiency. We are developing “ physical local training” algorithms that are more compatible with broken-isomorphism physical neural networks. This is particularly well suited for performing machine learning tasks with arbitrary analog devices as shown in an article from our lab published in Science by Momeni et al [1] (link below).
On the hardware side, we are focusing on wave-based systems in acoustic, microwave, and optics. For example in our optical setup, we are elaborating a monochromatic optical setup that mimics the propagation of optical waves in a bulk material with scattering and nonlinear elements. The propagation in such a device mimics a neural network. The weighted sum of each neuron is provided by diffraction and superposition of waves while the nonlinearities correspond to light-matter interactions (see Figure 1 below).
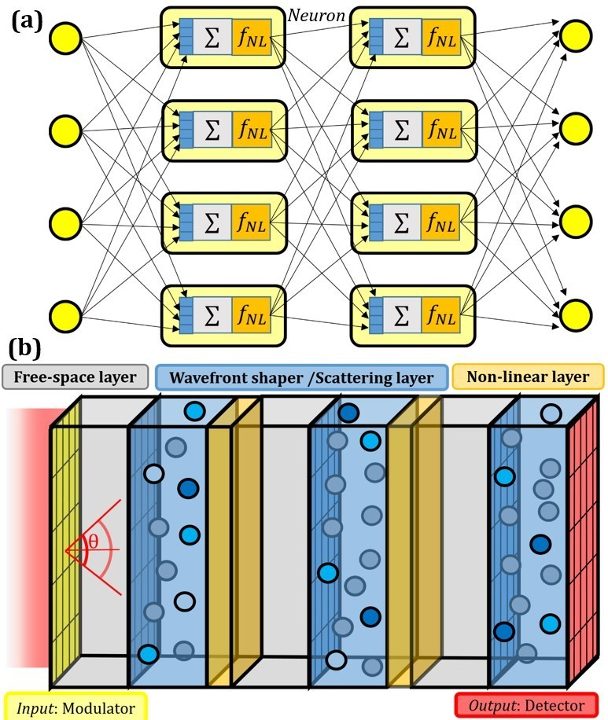
(a) A neural network made with two layers (b) A layered structured medium to mimicks the neural network with light.
To learn more
- A. Momeni, B. Rahmani, M. Malléjac, P. del Hougne and R. Fleury, “Backpropagation-free training of deep physical neural networks“, Science 382, 6676, 2023.
- X. Lin, Y. Rivenson, N.T. Yardimci, M. Veli, Y. Luo, M. Jarrahi, A. Ozcan “Alloptical machine learning using diffractive deep neural networks “, Science 361, 2018.
- P.L. McMahon, “The physics of optical computing“, Nature Physics 5, 717-734, 2023. [4] J. Sol, D.R. Smith, P. del Hougne, “Meta-programmable analog differentiator“, Nature Communications 13, 1713, 2022.
- F. Xia, K. Kim, Y. Eliezer, L. Shaughnessy, S. Gigan, H. Cao, “Deep Learning with Passive Optical Nonlinear Mapping“, ArXiv, 2307.08558v2, 2023.
- Momeni, A., Rahmani, B., Scellier, B., Wright, L. G., McMahon, P. L., Wanjura, C. C., … & Fleury, R. (2024). Training of Physical Neural Networks. arXiv preprint arXiv:2406.03372.
Involved LWE researchers
Ali Momeni (Ph.D. student)
Tim Tuuva (Ph.D. student)
Guillaume Noetinger, Janez Rus (postdoctoral researchers)
Haiwei Wang (Master project)
Collaborators
Philipp del Hougne, CNRS IETR