Our research focuses on the interaction of electromagnetic fields with small dimension systems compared to the wavelength. In practice, those systems range from a few nanometers to several micrometers. In addition to experimental work, we are developing sophisticated modelling techniques to solve Maxwell’s equations with the formalism of the Green’s tensor. These methods are particularly well suited for the modelling of geometries that incorporate scatterers embedded in stratified backgrounds, as illustrated in the following figure.
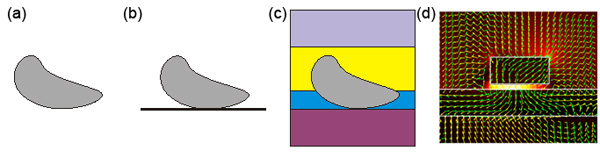
This previous figure shows the evolution of the modelling techniques developed at the NAM: (a) scatterer in infinite homogeneous space, (b) scatterer on a surface, (c) scatterer in a stratified medium. This last situation is illustrated in (d), which shows the computation of the interaction between a gold nanoparticles and a gold thin film, leading to a very strong field enhancement at their interface. For that 3D calculation, only the particle volume had to be discretized; the rest of the system – including the complex stratified background with the thin metal film – was handled semi-analytically using the corresponding Green’s tensor.
More recently, we have moved one step further by developing a surface integral technique that requires only the surface of the scatterer to be discretized. This dramatically increases the performance of the technique since the numerical requirements scale with the surface of the scatterer, not its volume anymore. Furthermore, using a triangular mesh and finite elements basis functions that already partly fulfill Maxwell’s equations, we were able to handle analytically the singularity of the Green’s tensor, hence producing a very stable algorithm. Furthermore, this approach can be used to compute the field at very short distances from the scatterer, which is important to investigate effects such as plasmon-enhance Raman scattering of fluorescence. Finally, the triangular finite elements mesh makes possible the modelling of realistic scatterers, such as the plasmonic antenna shown in the following figure, whose discretized geometry (middle) was derived from the electron microscopy image on the left. The right part of the figure shows the field intensity in and around the antenna when it is excited at its resonance.

This technique has also been extended to compute light scattering in periodic geometries in 1, 2 and 3 dimensions, by merely discretizing the surface of a single scatterer, as illustrated in the following figure which shows a typical example where light is scattered by a photonic crystal made with an infinite square array of pillars with a refractive index of 3.36 in air. Panels (a) and (b) consider no substrate, while (c) and (d) include a substrate. Different illumination wavelengths λ are considered: (a) λ=350 nm, (b) λ=700 nm, (c) λ=340 nm, (d) λ=700 nm.

Metasurfaces design
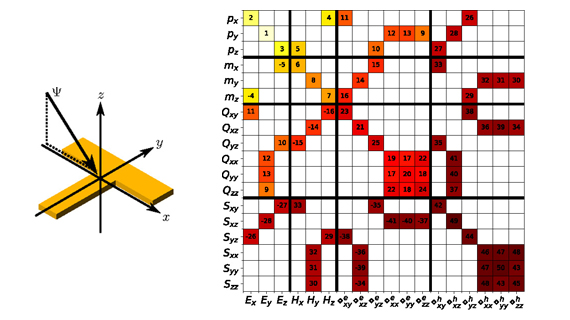
The modelling activities in the NAM support our experimental research. For example, different techniques have been developed to design metasurfaces, e.g. by connecting the spatial symmetries of a metasurface to its material parameter tensors and its scattering matrix. This provides a simple yet effective way to effortlessly determine properties of the metasurface scattering response, such as chirality or asymmetric transmission, and which of its effective material parameters should be taken into account in the prospect of a homogenization procedure. The following figure illustrates this approach for a metasurface built from a square array of T-shaped nanostructures illuminated under oblique incidence. The matrix shows which multipoles (up to the quadrupoles) exist in the response of that system.
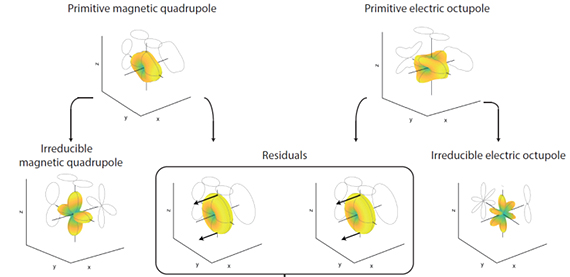
Multipoles analysis is ubiquitous in the study of many electromagnetic problems, including the design of metasurfaces or the analysis of light scattering. In spite of their popularity in our research community, the multipoles zoology is far from trivial since many different multipole families exist. This complexity is also of interest to us and we study the relationship between different families of multipoles, as illustrated in the following figure, where so-called toroidal multipoles emerge as the residuals obtained from the “normalization” of primitive multipoles into irreducible multipoles.