Analytical Modeling

Analytical modelling, as simple and computationally affordable tools, is widely used in optimizing the layout and control of the wind farms. Despite being less accurate than more advanced turbulence-resolving numerical schemes, analytical models have the added value of providing fundamental insight into the physics, as their derivation relies on the basic equations governing the conservation of flow properties. This fundamental basis for modeling provide a broad area of interest in the field and can cover a wide range of applications: from single turbine wake modeling to superposition of wakes in a wind farm, from the wake flow analysis over topography to the interaction of wake flow with the atmospheric boundary layer.

In WiRE, the development of comprehensive and robust analytical models is of great interest to improve the understanding of the wind turbine/farm flow and push the limits of optimization. Top-level experimental facilities and in-house numerical tools provide the unique ground to validate the analytical frameworks against various scenarios. In this context, followings are some of the key analytical models developed in the Lab:

Gaussian wake model: Originally proposed by Bastankhah and Porté-Agel (2014) as an alternative to the top-hat assumption for the wake velocity deficit. The derivation assumes an axisymmetric self-similar Gaussian distribution for the wake flow. The model was extended to include effect of non-axisymmetric wake flow (Abkar and Porté-Agel (2015a)), vertical wind veer (Abkar et al. (2018)), and Yaw misalignment (Bastankhah and Porté-Agel (2016)). 

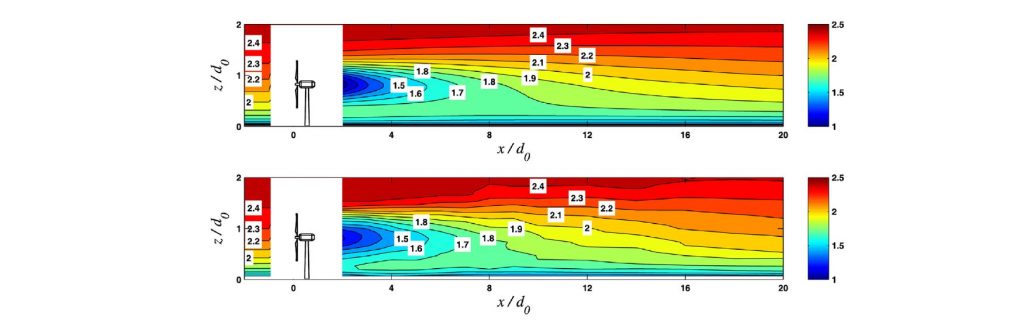
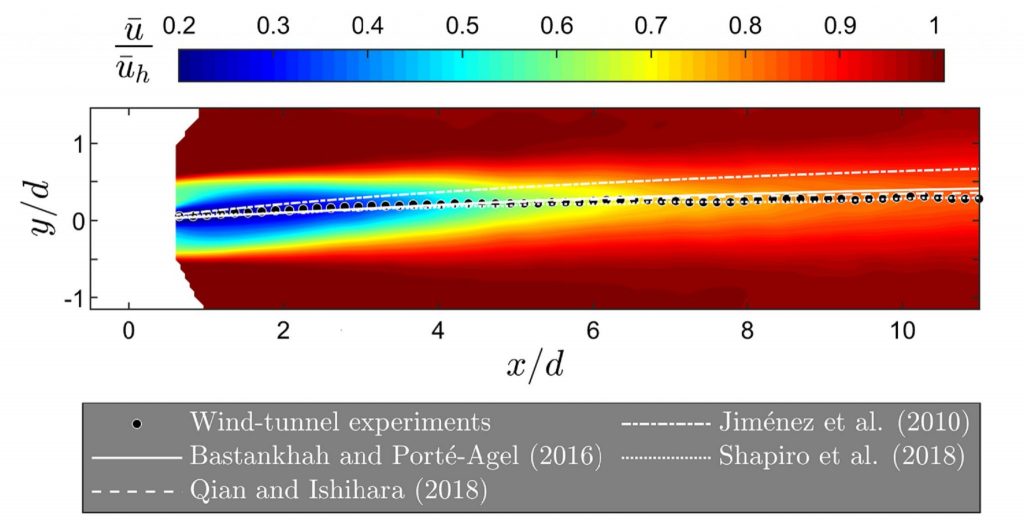
Contours of streamwise velocity in the vertical plane normal to the wind turbine, at zero span: New proposed model (top) and wind-tunnel measurements (bottom)
Contours of the normalized streamwise velocity component on a horizontal plane at hub height for a yawed turbine with γ = 20◦ obtained with wind-tunnel measurements. Comparison of wind tunnel wake center with different analytical models

Momentum-conserving wake superposition method: As a key element in wind farm analytical modeling, an accurate scheme for wind turbine wake superposition is a fundamental element. To address this and to conserve the streamwise momentum in the wind farm, a new superposition framework is proposed to calculate the contribution of each wake in the total wake velocity deficit. Beside conserving the total streamwise momentum, this model provides accurate prediction for the wind farm power.

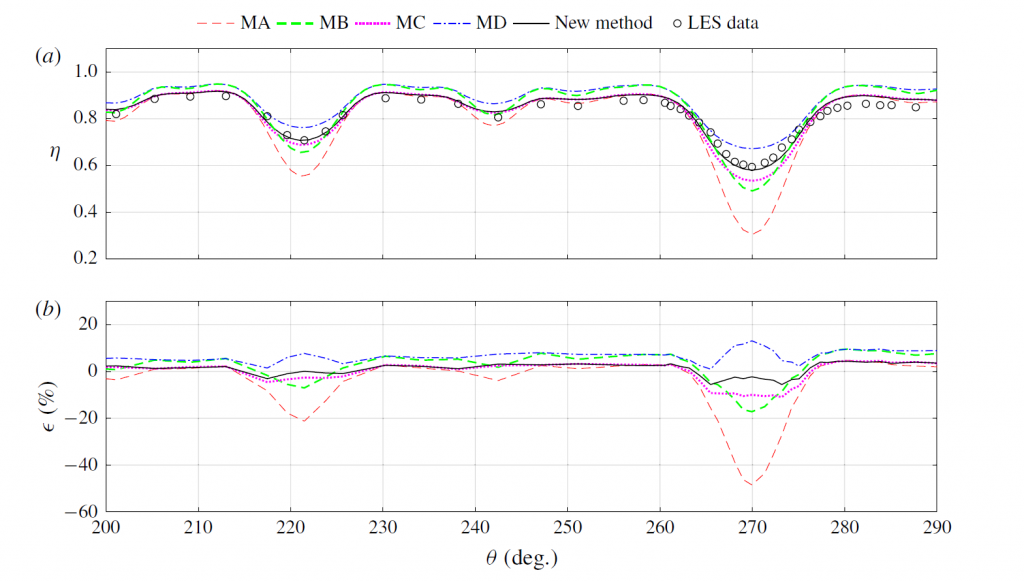
Wake Superposition
(a) Comparison of the Horns-Rev wind farm efficiency predicted by different wake superposition methods (MA: Lissaman (1979), MB: Katic et. al (1987), MC: Niayifar & Porté-Agel (2016), MD: Voutsinas et. al (1990)) versus the wind direction, with 270 corresponding to western winds. (b) Relative error between the model predictions and the LES data at different wind directions.

Pressure gradient model: Considering wind farm operation on the topography, this model aims to predict effect of pressure gradient on the evolution of turbulent axisymmetric wake, with a particular focus on the evolution of the maximum velocity deficit and wake width compare to the case with zero pressure gradient.  

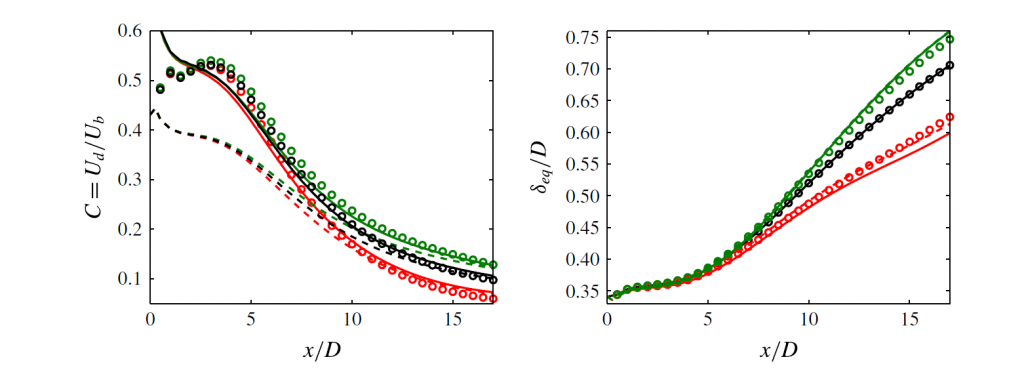
Pressure Gradient Model
Normalized maximum velocity deficit (left) and wake width (right) as a function of the streamwise distance for the Zero (black), Favorable (red) and Adverse (green) pressure gradient cases. Comparison of LES (circles), model (solid lines), and asymptotic solution (dashed lines).

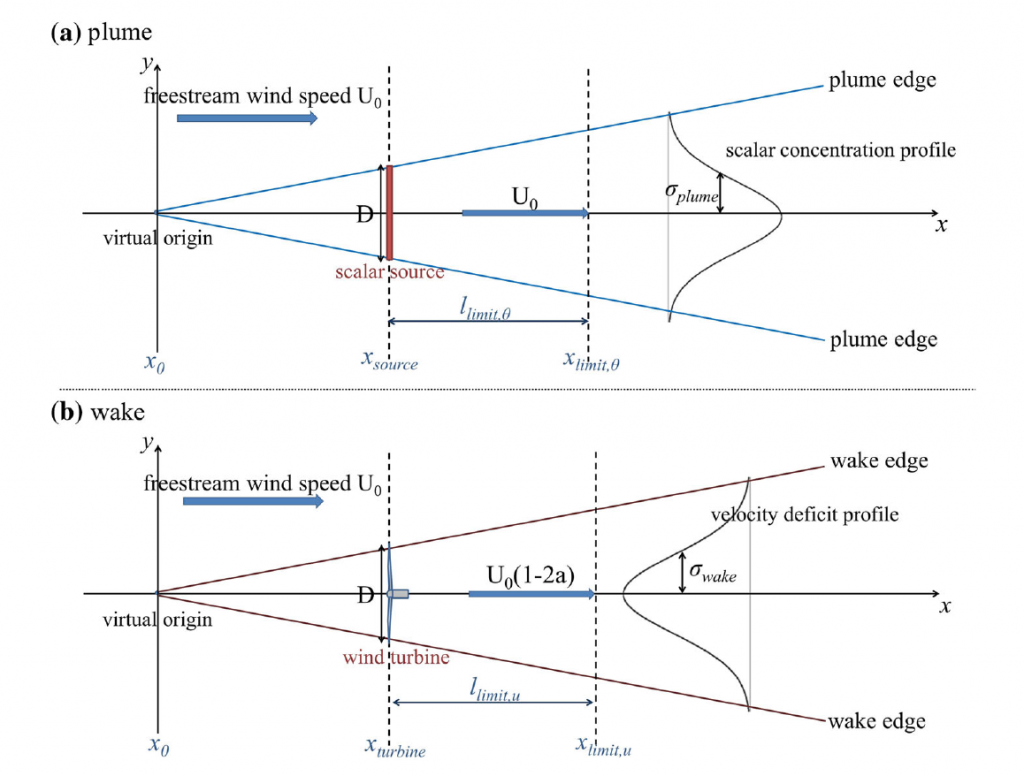
Analogy of wake and diffusion: Similarities among the passive scalar transport in the atmosphere and wind turbine wake leads to a new modeling framework for the wind turbine wake growth rate estimation. This approach profits from the analogy between wake expansion and scalar dispersion in the turbulent flow and provide a simple physical model for the wake growth rate.

Analogy of wake and diffusion
Schematics for the lateral scalar plume dispersion from an area source (a), and the lateral wake expansion behind a wind turbine (b).

References: