From scratch to supercomputers: building a large-scale strong lensing computational software bottom-up
The goal of this project is to modernize the gravitational lensing code Lenstool developed by Prof. Jean-Paul Kneib from the LASTRO group at EPFL using a bottom up approach in order to run on current massively parallel supercomputers such as CSCS’ Piz Daint.
High performance bottom-up codes are constructed by focusing on HPC first principles, such as core/node performance, and focus on algorithms and ad-hoc data structures first. Then, performance is gradually scaled using vectorization, concurrent and distributed techniques to reach its peak performance.
This leads to highly specialized codes with reduced development time and time-to-solution in order to maximize scientific throughput and discoveries.
Scientific relevance

Twin QSO (center), Credit: ESA/Hubble & NASA
Lensing is the light refraction that focuses or disperses light beams caused by an optical device (e.g. glass).
Gravitational lensing is the light refraction caused by a distribution of matter according to Albert Einstein’s general theory of relativity (1916)
- Article about star General Relativity in 1936 (A. Einstein, Science)
- Fritz Zwicky posited in 1937 that the effect could allow galaxy clusters to act like lenses
- First observed in 1979 “Twin QSO” SBS 0957+561
Optical artifacts are created by dense mass distributions (galaxies, dark matter, black holes).
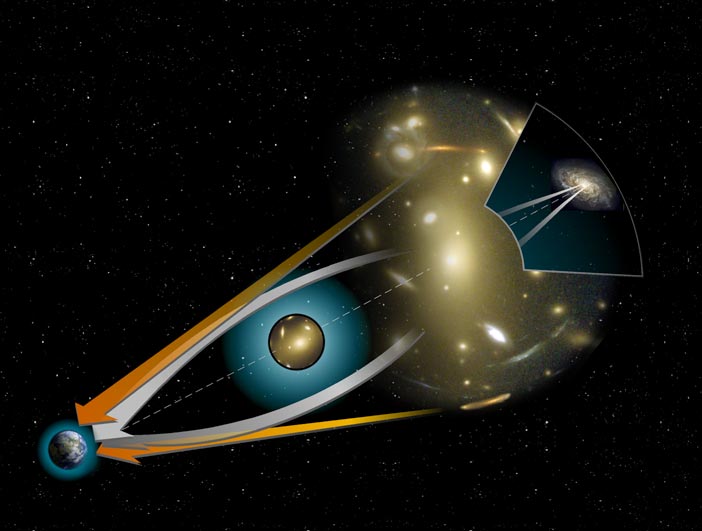
Gravitational Lensing, Credit: Wikipedia
We use a parametric lens model with:
- ε the ellipticity of the projected mass distribution
- ω the finite core radius
- κ0 the normalized surface mass density
- (x,y) the lens position
The main idea is to reverse engineer the lenses, i.e. compute the lenses’ mass and then recompose far-away objects.
The typical search space dimension is 1010.
Technical aspects
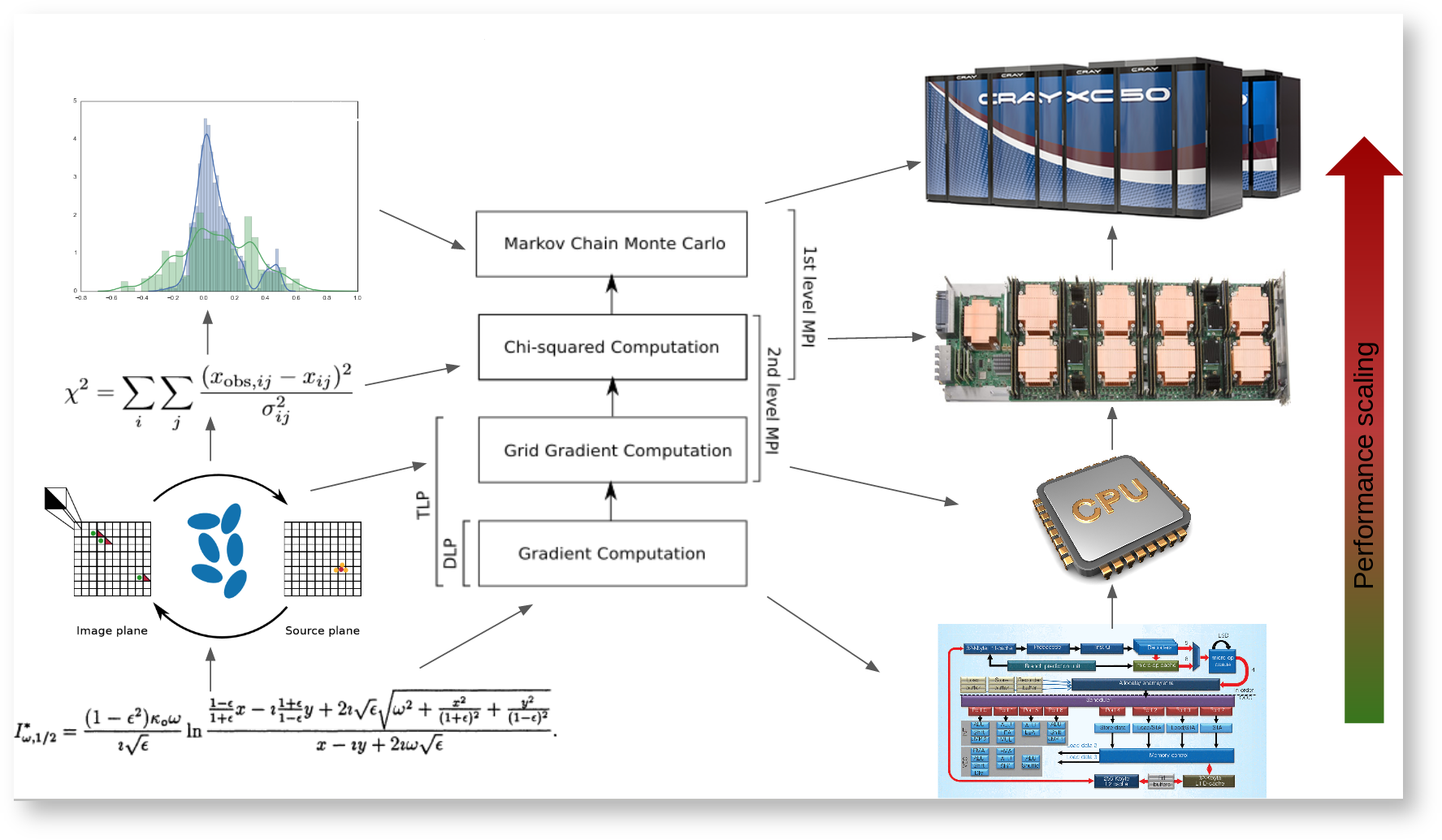
The algorithm can be described as follows:
Given a parametric model for all the lens types
Step 0: Compute all the gradients
- An example of gradient is:
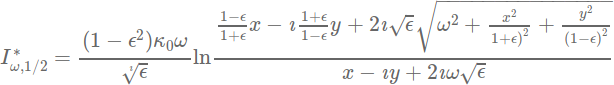
Gradient example: PIEMD (Kassiola, A. & Kovner, I. 1993)
Evaluating the gradient represents more than 90% of total time
Step 1: unlensing (linear transformation)
- lensing the green dots (images) to the Source plane (yellow dot)
- Compute the barycenter of the yellow dots
Step 2: relensing (non-linear transformation)
- Decompose the Image plane into triangles
- Lense the triangles to the Source plane
- If the lensed triangle includes the barycenter, a predicted image is found (red triangles in Image plane)
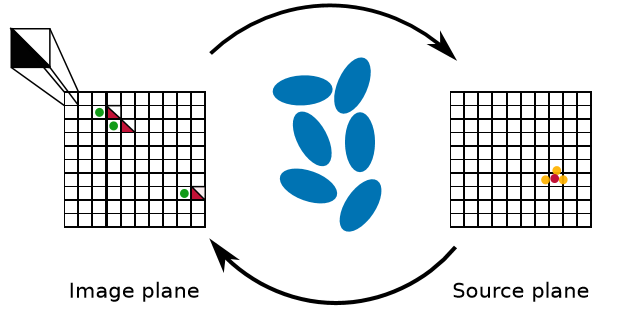
Step 3:
- Compute and pass
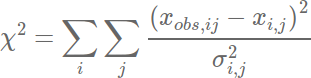
to a Bayesian Markov Chain Monte Carlo which returns a new set of parameters until close to reality.
Full algorithm: bottom-up approach, starting from core performance to full scale. Each algorithmic step is mapped to the ad-hoc hardware in order to scale performance (DLP, TLP, MPI).
Results
Grid Gradient benchmark
All results are expressed as Time To Solution in seconds.
Step 0
Gradient benchmark computation: 5000×5000 pixels image, 69 sources, 203 constraints
| Code | AVX2 | AVX512F | ||
|---|---|---|---|---|
| TTS | Factor | TTS | Factor | |
| Lenstool 6.8.1 | 1.0s | 1X | 4.8s | 1X |
| LenstoolHPC AOS | 0.8s | 1.3X | 5.6s | 0.9X |
| LenstoolHPC SOA | 0.5s | 2.0X | 3.3s | 1.4X |
| LenstoolHPC SOA + DLP | 0.2s | 4.5X | 0.4s | 11.4X |
- AVX2: Broadwell Intel Xeon CPU E5-2630 v4 @ 2.20GHz, intel compilers 17
- AVX512F: Intel Xeon Phi CPU 7210 @ 1.30GHz, intel compilers 17
Step 1
Single node Grid Gradient benchmark computation: 6000×6000 pixels image, 69 sources, 203 constraints.
| Code | AVX2 | AVX512 | SIMT | |||
|---|---|---|---|---|---|---|
| 2630v4 | 265v4 (PizDaint) | SKL Plat. 8170 HT | KNL (greina) | P100 (greina) | V100 | |
| lenstool 6.8.1 (TLP) | 11.5 | 9.3 | 8.6 | 10.7 | – | – |
| lenstool-HPC (SOA + TLP) | 5.6 | 2.1 | 1.8 | 5.8 | – | – |
| lenstool-HPC (SOA + TLP + DLP/SIMT) | 3.0 | 1.67 | 0.72 | 0.84 | 0.68 | 0.24 |
Comments:
- TLP is giving the best bang for your bucks
- SOA alone gives a nice boost (and is mandatory for efficient DLP)
- DLP is getting better with wider vector sizes (avx512 is ~2x avx2).
- GPUs performance is limited by the data transfer
Chi2 computation
Daint-GPU: Chi2 (Step 2) Strong Scaling
Scalability of the Chi2 benchmark using a 8k x 8k image, 69 sources, 203 constraints on Piz Daint multicore, 1 MPI process and 18 threads per socket, in seconds
| Num Nodes | Grid Gradient Comp | Quadrant unlensing (per MPI domain) | MPI reduction | TTS |
|---|---|---|---|---|
| 1 | 1.39 | 24.80 | 0.00 | 26.20 |
| 2 | 0.83 | 12.40 | 0.00 | 13.30 |
| 4 | 0.54 | 6.21 | 0.00 | 6.79 |
| 8 | 0.41 | 3.12 | 0.00 | 3.57 |
| 16 | 0.34 | 1.57 | 0.00 | 1.96 |
| 32 | 0.30 | 0.81 | 0.00 | 1.14 |
| 64 | 0.28 | 0.40 | 0.00 | 0.77 |
| 128 | 0.27 | 0.33 | 0.00 | 0.66 |
| 256 | 0.28 | 0.17 | 0.01 | 0.56 |
| 512 | 0.30 | 0.12 | 0.01 | 0.61 |
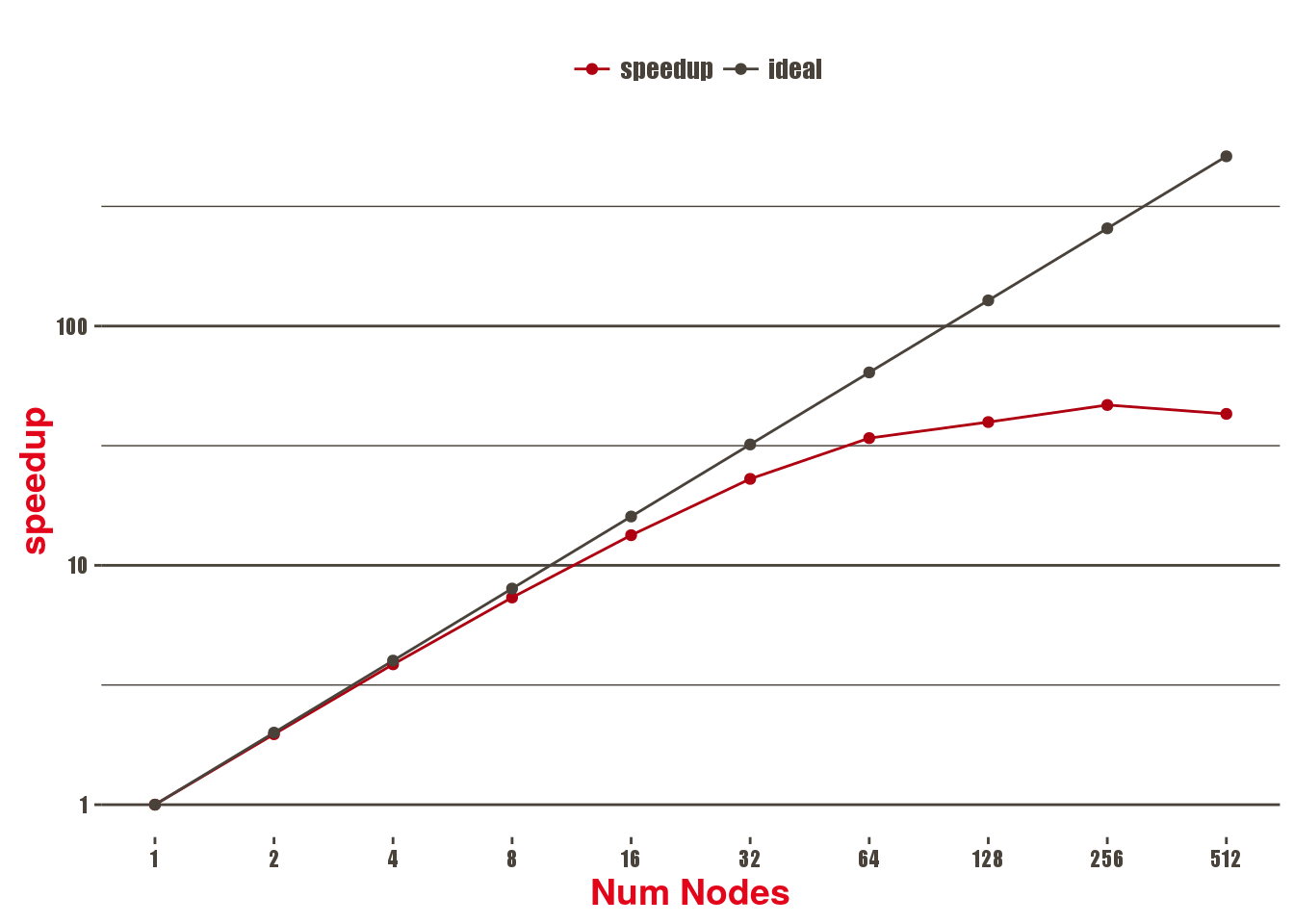
Remarks:
Grid Gradient Comp is the first part that stops scaling (at 32 nodes).
Daint-MC
Scalability of the Chi2 benchmark using a 8k x 8k image, 69 sources, 203 constraints on Piz Daint multicore, 1 MPI process and 18 threads per socket, in seconds.
| Num Nodes | Grid Gradient Comp | Quadrant unlensing | MPI reduction | TTS |
|---|---|---|---|---|
| 1 | 10.51 | 19.25 | 0.00 | 29.83 |
| 2 | 5.24 | 10.11 | 0.06 | 15.45 |
| 4 | 2.74 | 4.87 | 0.11 | 7.75 |
| 8 | 1.41 | 2.51 | 0.01 | 3.95 |
| 16 | 0.75 | 1.41 | 0.03 | 2.20 |
| 32 | 0.43 | 0.72 | 0.01 | 1.17 |
| 64 | 0.24 | 0.37 | 0.01 | 0.63 |
| 128 | 0.14 | 0.20 | 0.02 | 0.37 |
| 256 | 0.14 | 0.12 | 0.04 | 0.31 |
| 512 | 0.45 | 0.09 | 0.14 | 0.69 |
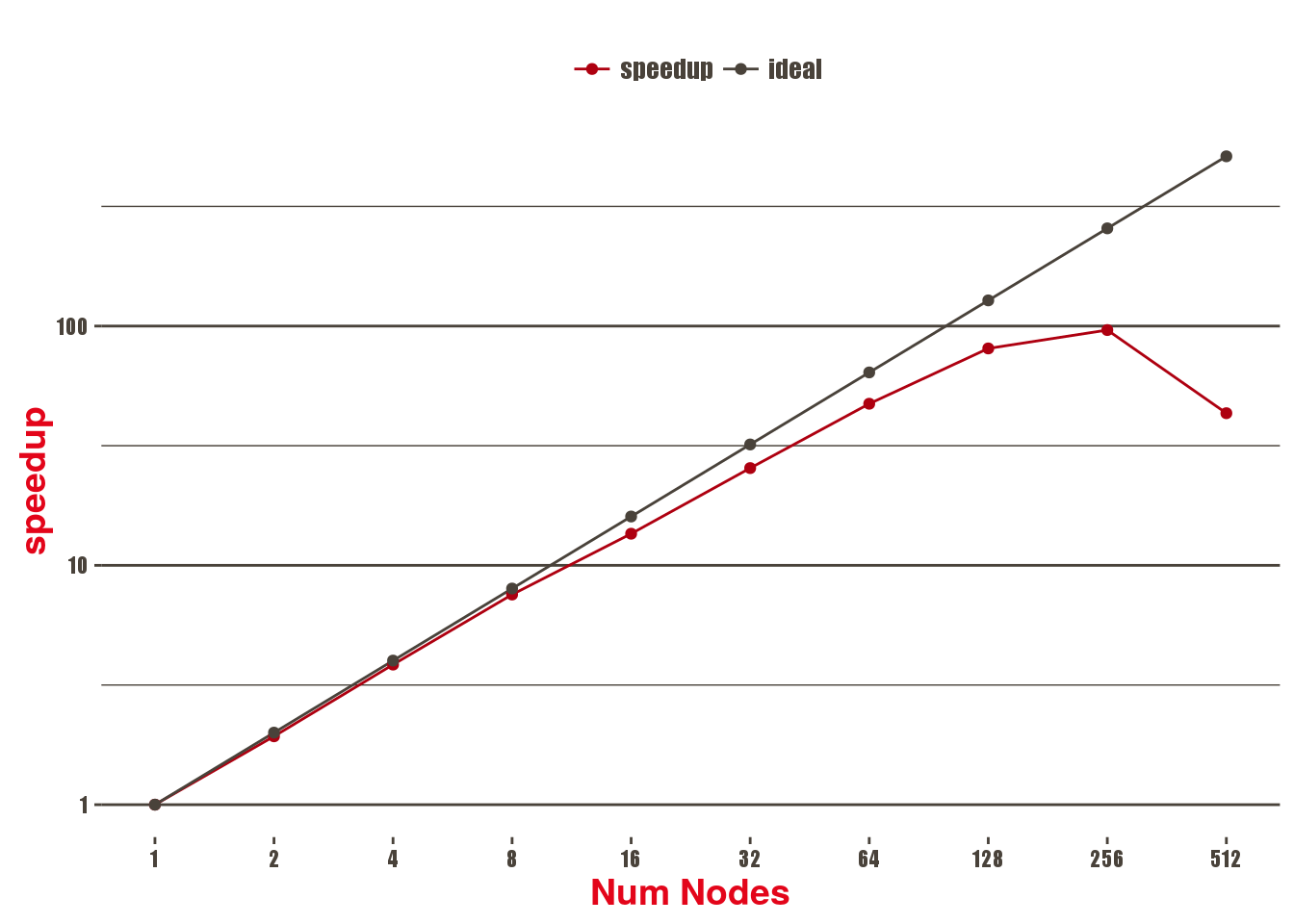
Remarks:
Grid Gradient Comp is the first part that stops scaling (at 256 nodes).
Bottom line
This represents a 50X compared to Lenstool 6.8.1 in 6 months FTE.
The work done by SCITAS was financed by FSB.
Used software
The HPC clusters at SCITAS use the Slurm workload manager in order to dispatch jobs.
Development
- Code on c4science, with unit tests for each kernels (lensing, unlensing, Chi2…)
- Small development project on CSCS’ Grand Tave (KNL) for further tuning
- Large development project submitted for CSCS’ Piz Daint – Aries network tuning – GPU tuning: lensing, unlensing and chi computation are (very) regular
- Development a parallel MCMC framework, could lead to a 500X speedup.
Pi4u: http://www.cse-lab.ethz.ch/research/projects/pi4u/ (P. E. Hadjidoukas et al., ETHZ)
Papers
- High Performance Computing for gravitational lens modeling: single vs double precision on GPUs and CPUs
Markus Rexroth, Christoph Schafer, Gilles Fourestey, Jean-Paul Kneib
To be submitted - High Performance Strong Lensing Map Generation for Lenstool
Christoph Schafer, Gilles Fourestey
In Preparation