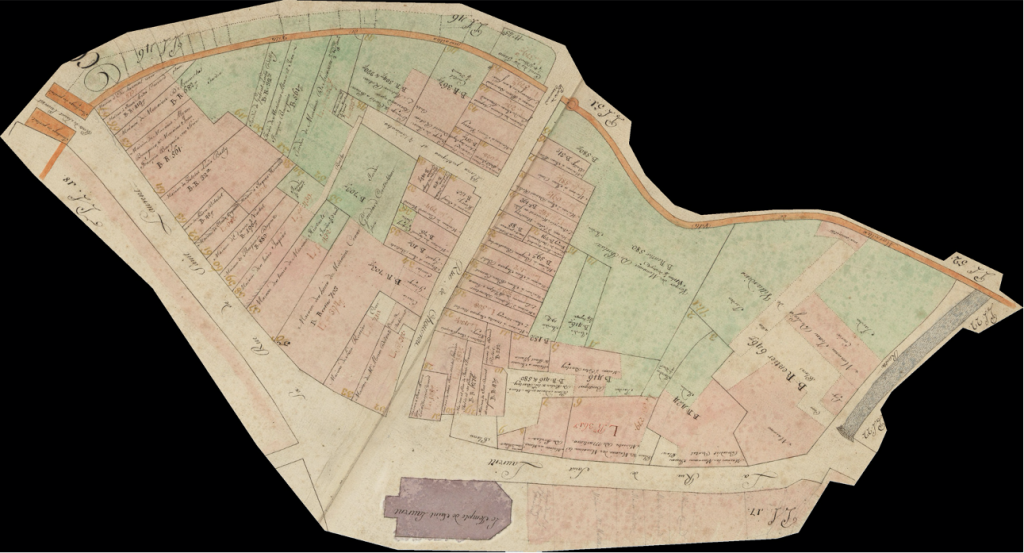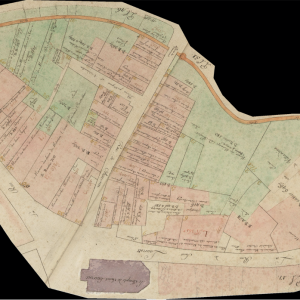
Cadastral maps are among the most complex structured historical representations, hence the late appearance of this technology. The wealth of information in these sources makes them indispensable for digital humanities and historical reconstruction. Moreover, the mathematical nature of cartography makes it easily compatible with the computational world. For several years now, historians and geographers have been working on vectorizing historical maps by hand. The vectorization process consists of redrawing one by one the geometric elements of the map (roads, parcel boundaries, buildings, etc.) in a geographic information system (GIS). In a second step, attributes can be added to this computer representation of the map, such as parcel numbers. This process ultimately makes the historical map digitally intelligible and, above all, searchable. For example, maps found in search engines such as Google maps, Mapbox or OpenStreetMap are vector maps. The problem, therefore, if we want to create databases that allow us to retrieve and access geohistorical information, is mainly a vectorization problem. It should be noted that, while this task is technically possible with today’s technology, the manual vectorization of a historical map is an extremely long process, usually taking several weeks for a single map. Therefore, in view of the hundreds of thousands of existing sheets, extracting the totality of the geodata from the past by hand is simply not realistic.
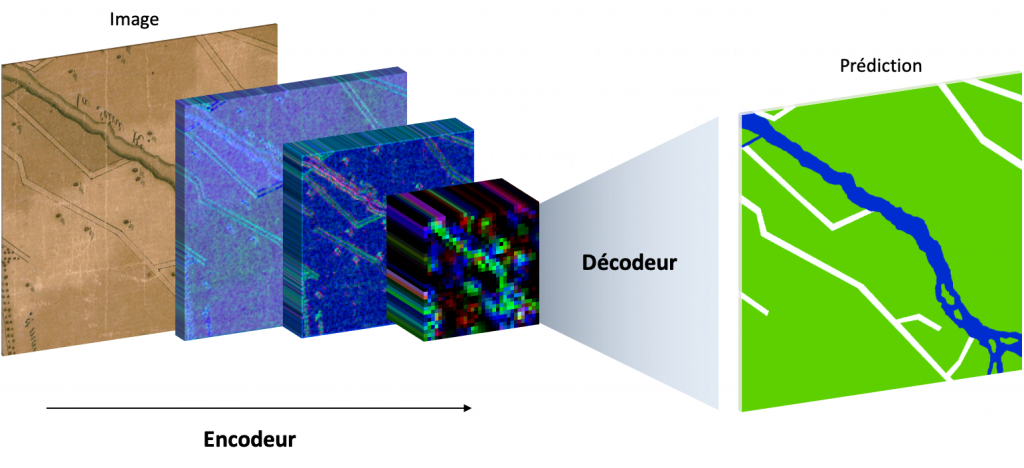
In 2019, Oliveira, di Lenardo, Tourenc and Kaplan proposed a revolutionary new method to automatically vectorize Napoleon’s Venice cadastre using artificial intelligence (AI) technology based on convolutional neural networks. Behind this term lies a mathematical object composed of numerous functions, each of which includes thousands of variables. Each variable is potentially coupled to a coefficient, called a weight. In a very intuitive way, it is possible to adjust these weights with great sensitivity to solve almost any image recognition problem, or more complex problems, such as the segmentation of objects or image semantics. It is the ability to solve the latter kind of problems that is used to segment historical maps. To achieve this result, it is necessary to train the network so that the variables learn to solve the desired task. This phase of training is very intuitive because it simply consists of presenting a relatively large number of examples to the network, containing both the question –in our case a map extract– and the expected solution –in the present case, the semantic segmentation of the various elements, which can simply mean coloring the buildings with one color and the road network with another color. Little by little, as the neural network learns from the examples, it becomes capable of solving the problem itself on maps it has never seen.
Most surprisingly, neural networks are able, when forced to, to understand complex concepts of morphology, topology and semantic hierarchy. These very advanced concepts allow AI to identify the buildings on a map that offers no visual clues other than contours, for example a black & white non-textured map. Thus, it is possible to train generic networks that are able to read just about any city map. On the other hand, it is also possible train specialized networks on maps whose grammar and representation are regulated, such as the Napoleonic cadastre.
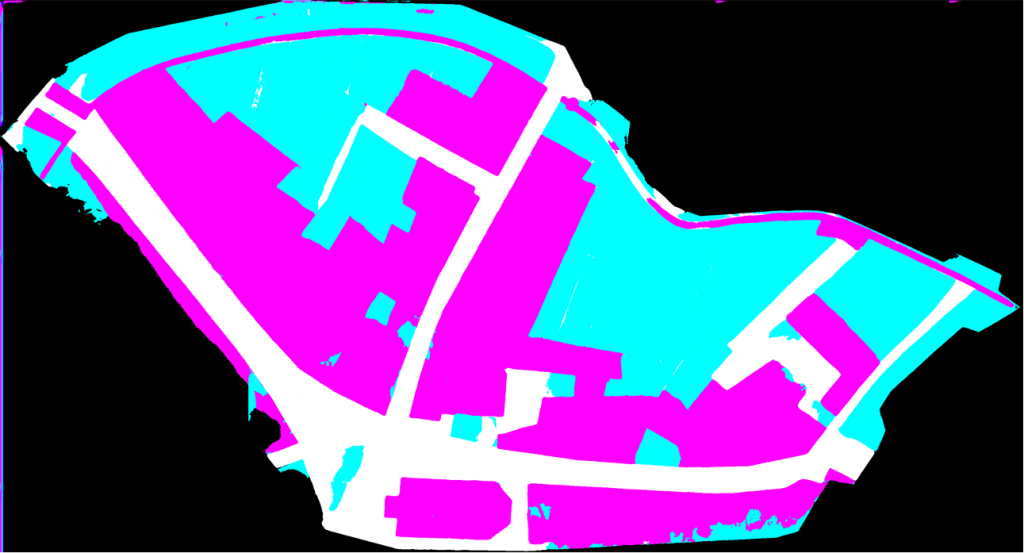
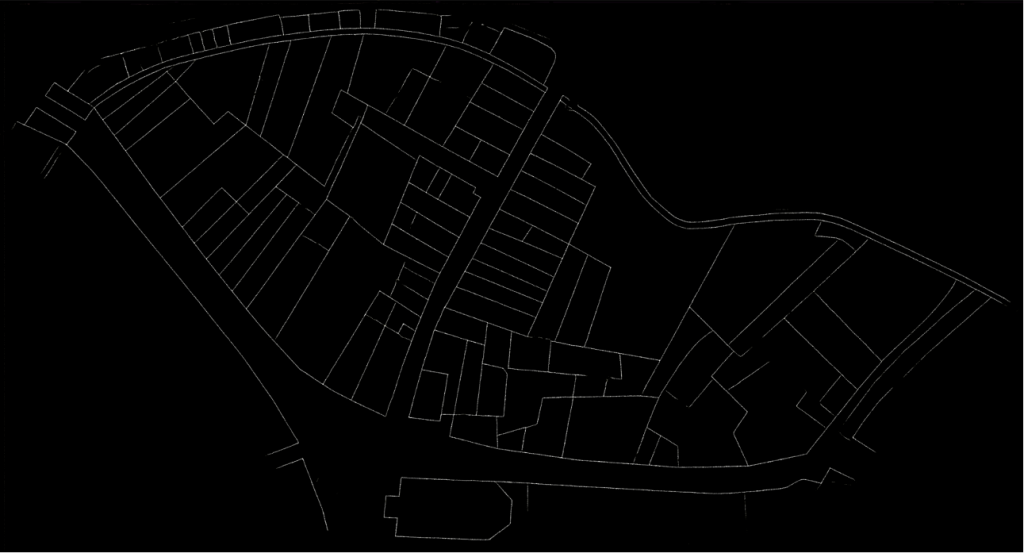
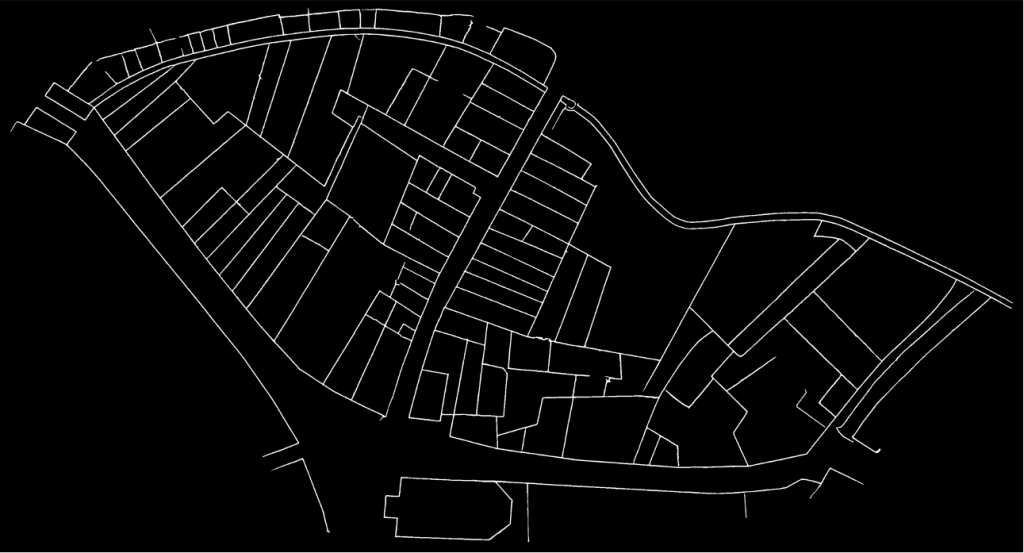
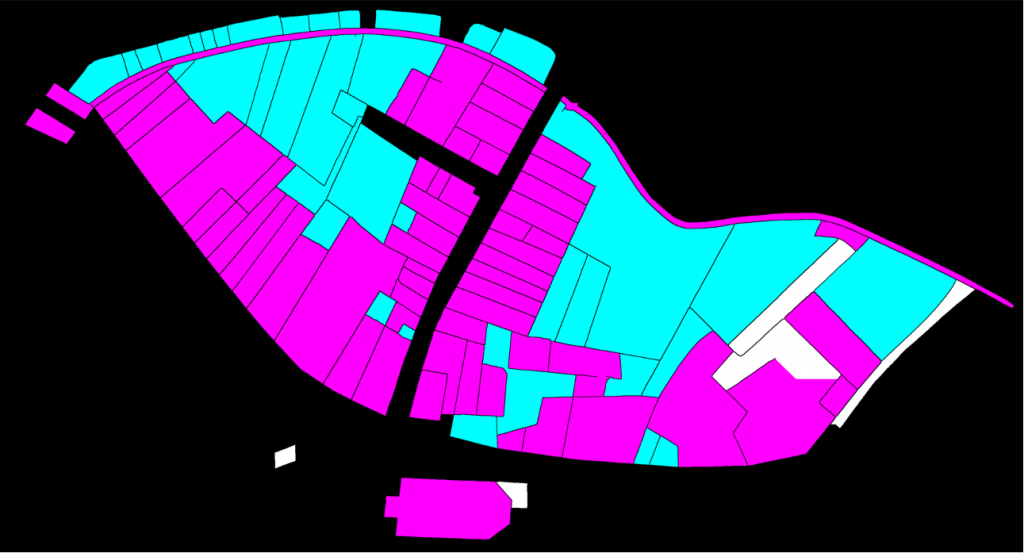
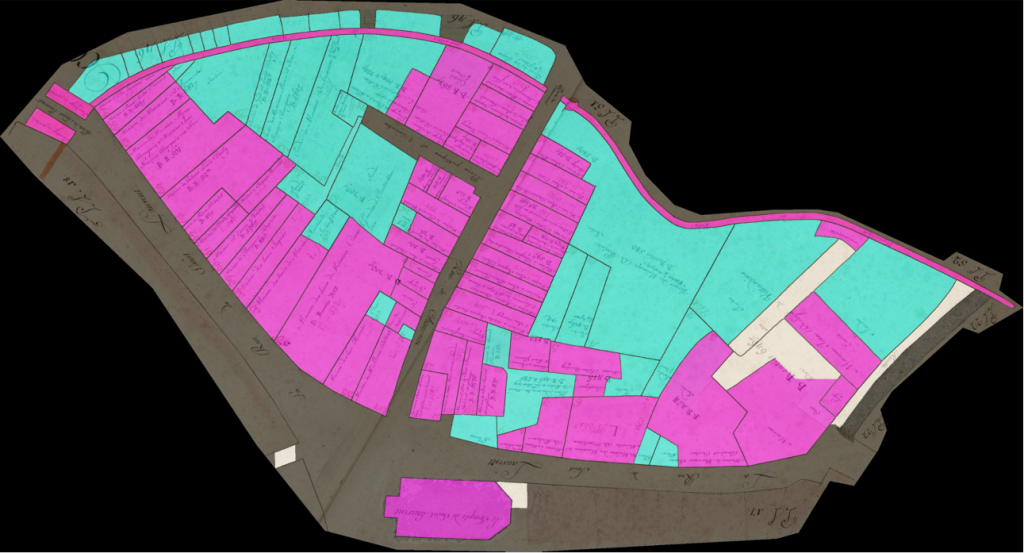
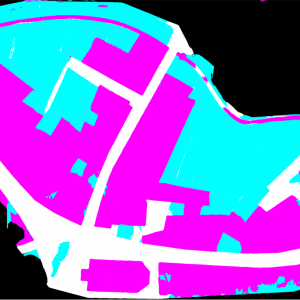
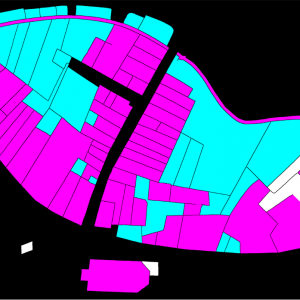
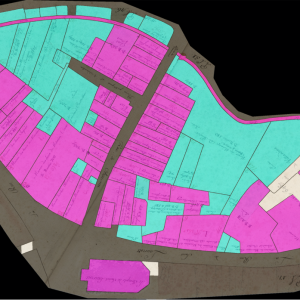
A strategy, consiting in pre-training the network on a generic corpus before forcing the latter to specialize was used to vectorize Lausanne Berney’s 1831 and Melotte’s 1727 cadastres. Several hundred figuratively heterogeneous maps of the city of Paris initially allowed the neural network to acquire representational flexibility and to integrate complex topological notions. In a second step, a limited number of examples extracted from each of the two cadastres of Lausanne were produced manually and very good predictions were quickly delivered by the network. The vectorization problem is divided into two sub-problems. The first one aims at identifying the contour of the represented objects, and thus at cutting out the parcels of land. The second problem aims at semanticizing the parcels, by identifying them as part of the built-up area, of the road network, of the unbuilt area, as a body of water or as non-mapping content (e.g. the frame of the sheet on which the map is drawn). A third neural network (Sasaki 2017) is also used to complete potentially misrecognized or interrupted lines.
To conclude, coupled with adapted post-processing based on the watershed algorithm and superpixels merging, this method has enabled us to efficiently vectorize, by annotating about 5% of the corpus, more than 94% of the plots of the Berney and Melotte cadastres, and thus to obtain a digital version of these historical documents that can be used for reconstitution, but also for urban analyses on the development of the city, as well as its organization and morphology.
For further information
Petitpierre, Rémi. “Neural Networks for Semantic Segmentation of Historical City Maps: Cross-Cultural Performance and the Impact of Figurative Diversity,” 2020. https://doi.org/10.13140/RG.2.2.10973.64484.
Petitpierre, Rémi. “4000 cartes par jour : des réseaux de neurones artificiels pour récupérer les géodonnées du passé.” Billet. Carnet de la recherche à la Bibliothèque nationale de France (blog), August 31, 2020. https://bnf.hypotheses.org/9676.
Ares Oliveira, Sofia, Isabella di Lenardo, Bastien Tourenc, and Frédéric Kaplan. “A Deep Learning Approach to Cadastral Computing.” Utrecht, Nederlands, 2019. https://dev.clariah.nl/files/dh2019/boa/0691.html.
Long, Jonathan, Evan Shelhammer, and Trevor Darrell. “Fully Convolutional Networks for Semantic Segmentation.” ArXiv:1411.4038 [Cs], March 8, 2015. http://arxiv.org/abs/1411.4038.
Sasaki, K., S. Iizuka, E. Simo-Serra, and H. Ishikawa. “Joint Gap Detection and Inpainting of Line Drawings.” In 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 5768–76, 2017. https://doi.org/10.1109/CVPR.2017.611.