Initiation to the discovery of point group symmetry
Nicolas Schoeni and Gervais Chapuis
École Polytechnique Fédérale de Lausanne, Switzerland
The applet allows to study the symmetry operations of a small selection of polyhedra.
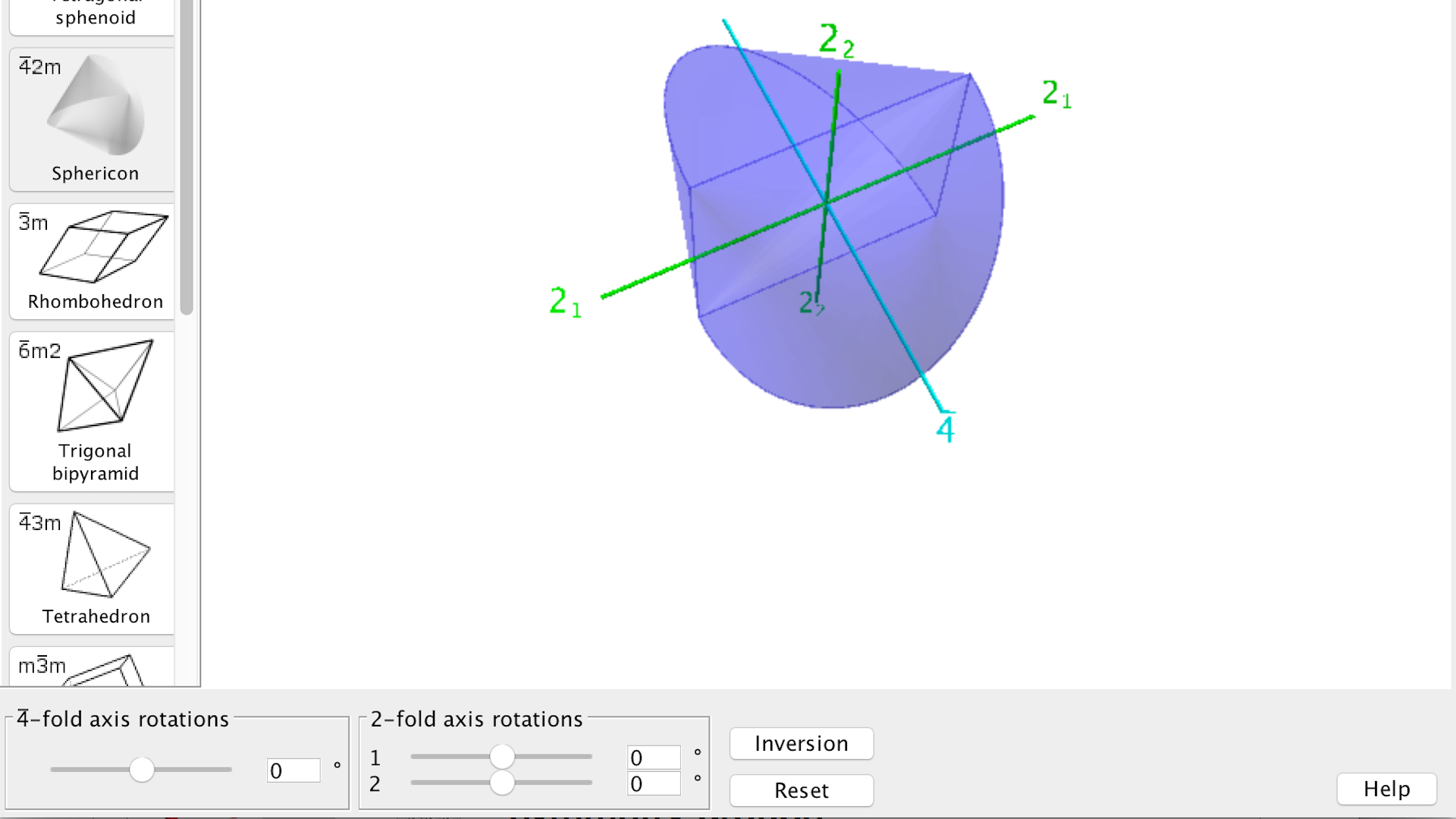
Every symmetry operation of an object (polyhedron, molecule, etc) which leaves at least one point invariant (i.e. unchanged) is described by its point group symmetry. If we limit ourselves to rotations of order 1, 2, 3, 4 or 6, we can find a total of 32 different groups, the so-called 32 point group symmetries.
The symbols of the 32 point groups in the international notation are given in the following table:
| Systems | point group |
|---|---|
| Cubic | m3m, 43m, m3, 432, 23 |
| Tetragonal | 4/mmm, 42m, 4mm, 422, 4/m, 4, 4 |
| Hexagonal | 6/mmm, 62m, 6mm, 622, 6/m, 6, 6 |
| Trigonal | 3m, 3m, 32, 3, 3 |
| Orthorhombic | mmm, mm2, 222 |
| Monoclinic | 2/m, m, 2 |
| Triclinic | 1, 1 |