Semester projects
Two semester projects are done in an EPFL research lab involved in computational sciences, at least one, outside the section of mathematics. Semester projects introduce student to R&D in Computational Science. They build largely upon the scientific and technical knowledge acquired during the curriculum and are meant to serve as a preparation for the Master’s research project. A Master’s teacher proposes a project topic and, together with the student, elaborates the project plan.
Please also visit the SMA webpage for projects
Offers
Usually, it is better to ask directly teachers in CSE if they have available projects.
The application process is similar to that of the master projects and is described here
Exemple semester projects CSE :
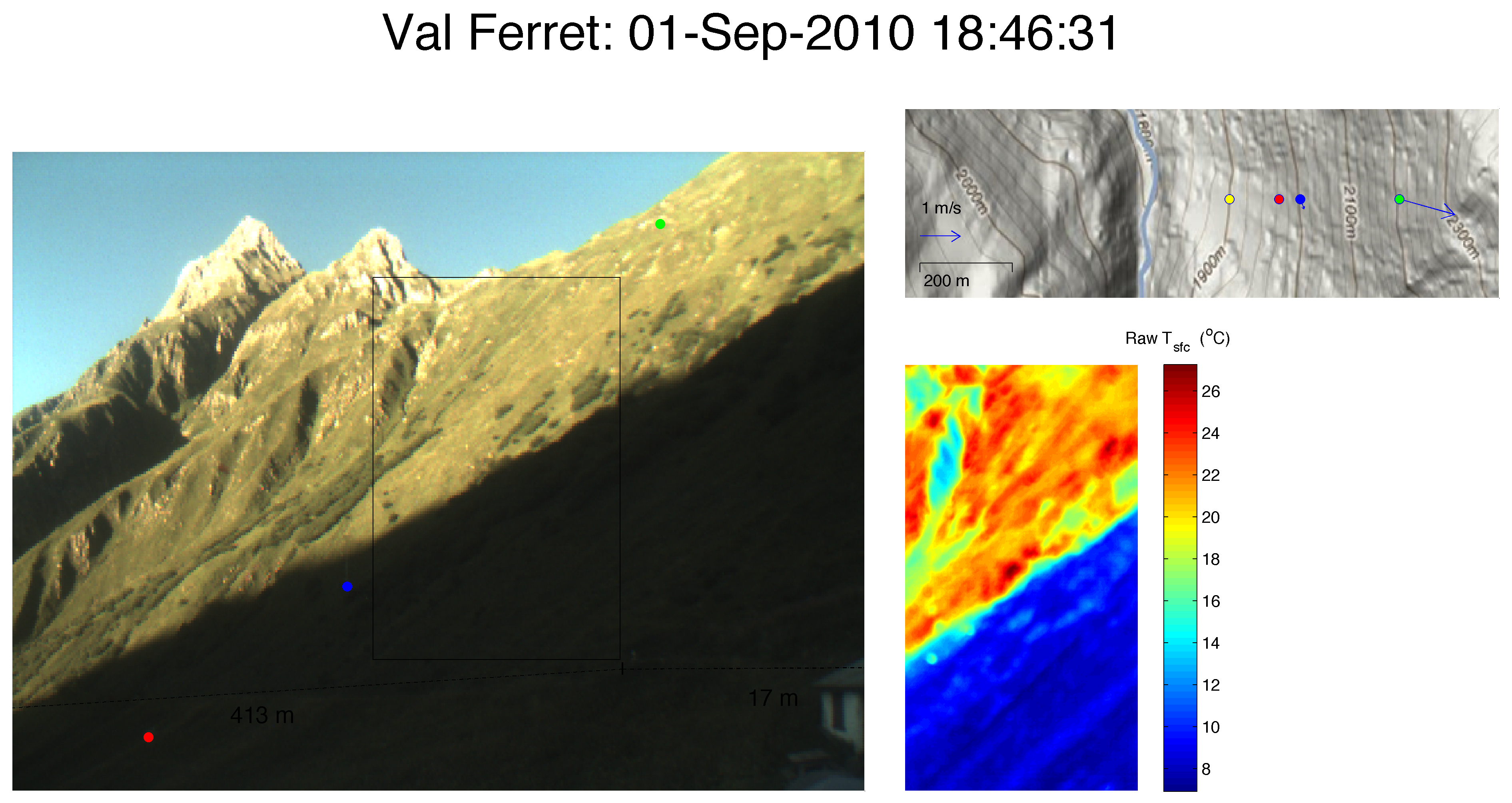
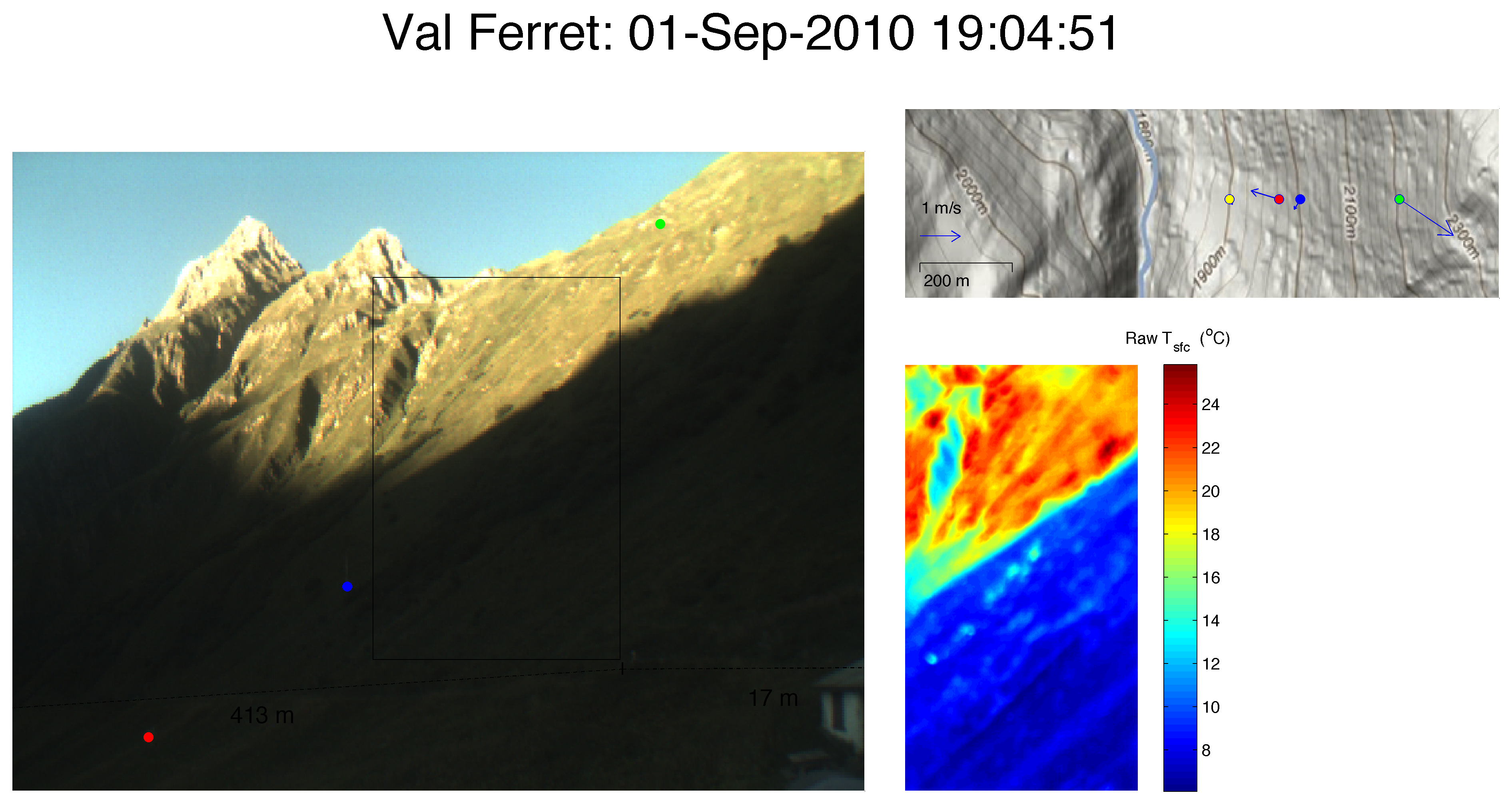
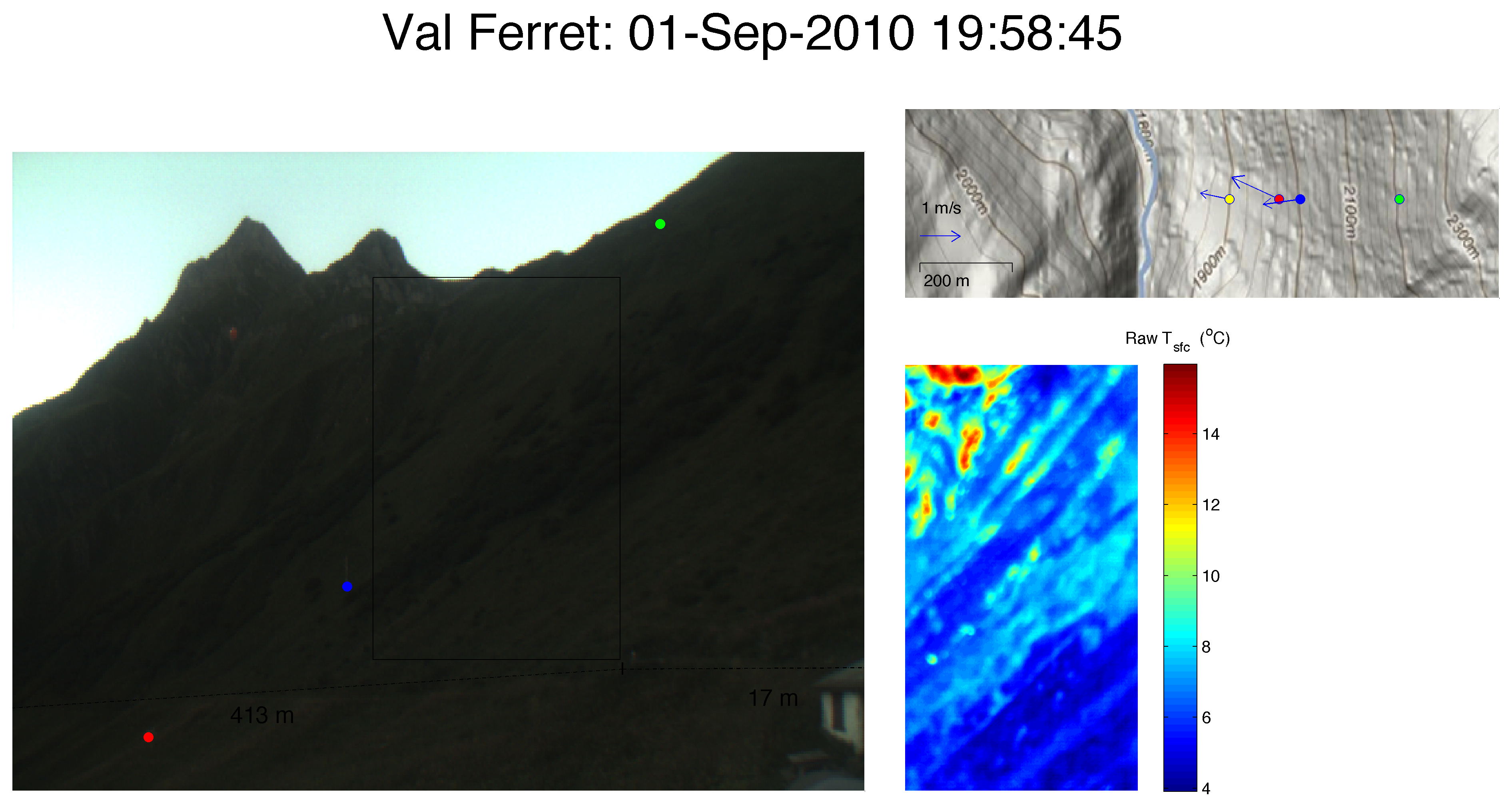
Eulalie SAUTHIER – The Impact of Surface Temperature on the Dynamics of Diurnal Mountain Winds over Steep Slopes
Responsible: Daniel Nadeau
Laboratoire de mécanique des fluides de l’environnement – EFLUM
Abstract:

Hainan HU – Systematic Exploration of Self-Assembling Robotic Systems using Webots
Professor: Alcherio Martinoli
Assistant: Grégory Mermod
Laboratoire de systèmes et algorithmes intelligents distribués – DISAL
Abstract
Self-assembly is the autonomous organization of components into patterns or structures without human intervention. Self-assembling processes are common throughout nature and technology. They involve components from the molecular (crystals) to the planetary (weather systems) scale and many different kinds of interactions. The concept of self-assembly is used increasingly in many disciplines, with a different flavor and emphasis in each.
We are currently looking for innovative methods for modeling the in-fluid self-assembly of micro scale components into complex, hybrid MEMS devices. The challenge posed by this task is two-fold: (1) one needs to account for the spatiality of the process (i.e., the position and the orientation of the building blocks with respect to each other and the geometrical features of the environment), and (2) self-assembly processes are intrinsically distributed and multi-scale, i.e., the involve a large variety of time- and length-scales, which need to be captured by the models.
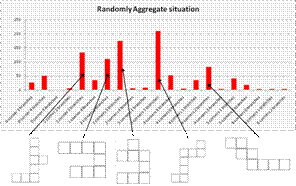
Aggregation property without rules
This project use existing building block model and environment model, modify the prototype of the building blocks, explored the position and the orientation of the building blocks with respect to each other and the geometrical features of the environment, the principles of the local grammars.
Since we have known the basic features of the self-aggregate, we can explore more and deeper by designing the aggregation. In this project, we design two algorithms: symmetric algorithm and generic algorithm, which use local grammar to achieve square aggregation. The yield of these two algorithm are 97.3%, 89.8% at least one square and 49.9%, 22.9% with two squares. From the result we can see that the high scalability is base on the sacrifice the yield. We also introduce a randomly check of the connectors method to see whether it will have a higher yield, but it doesn’t work for many reasons.
The advantage of global grammars is discussed in the situation that the aggregation shape is Nine-Square. The global grammar is just a supervisor which can collect the data that is hard for the building blocks to get with local grammars, and then use the data to set a sequence of rules to solve the troubles during the aggregation.

Aggregation into a square
Rui WANG – Implementation of Heat Transfer Model in a High-Performance Finite-Element Library
Professor: Jean-François Molinari
Project leader: Srinivasa Babu Ramisetti, Nicolas Richart, Guillaume Anciaux
Computational solid mechanics laboratory – LSMS
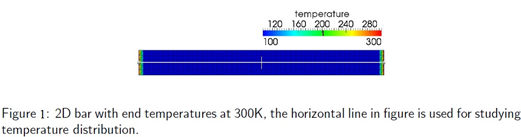
The objectives of this project are twofold. First, a generic (continuum) heat transfer model based on Fourier’s Law will be implemented within an object oriented finite element open source framework called AKANTU developed at the Computational Solid Mechanics Laboratory (LSMS). The implemented model will be useful to study both steady state and transient heat transfer problems. This work has to be validated by simulating various example problems such as thermal transfer in 3D cube. Second, I have reviewed current approaches for coupling a continuum description of heat transfer to an atomistic (Molecular Dynamics) description.
Some of the numerical results are shown below:
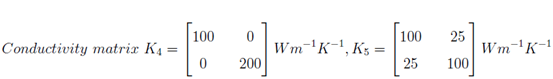
Vincent ZIMMERN – Stochastic Simulations of the MAPK Cascade
Professor: Vassily Hatzimanikatis
Laboratory of Computational Systems Biotechnology – LCSB
Abstract
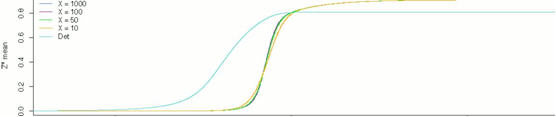
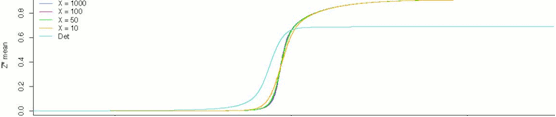
Figure 1: Stochastic Simulations of the MAPK cascade over 1000 s.
With the goal of achieving superior insight into the functioning of cellular signals, the systems biology community has been gradually increasing the realism and precision of its numerical simulations of cellular processes. After an initial period that saw the rise of continuous methods of approximation using systems of differential equations, the saga took an interesting turn when it was noticed that the continuity assumption underlying this dominant approach was far from being biologically valid. On the contrary, trace amounts of a single large biomolecule could have untold effects on larger signaling networks. As a result of this realization, the attention of the community gradually shifted towards stochastic methods that would take the inherent variability of these systems into account.
This project, following on the work of a master’s thesis completed in 2010 by Alen Brusjnak, attempts to simulate the tricyclic MAPK cascade, one of the most well-researched signaling cascades of the mammalian cell, using fully-stochastic methods. The results are analyzed in terms of the system’s ultrasensitivity. Much work remains to be done on this topic, but the paper concludes with some early findings that seem to confirm the inherent complexity of these signaling mechanisms. Below are some of the graphical results from the study.
 |
 |
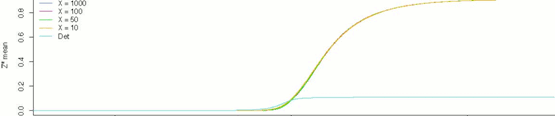 |
Figure 2: Results of stochastic simulations of the tricyclic MAPK cascade, 1000s.,
for different values of Michaelis-Menten constants
Nicolò PAGAN – Implementation of the point-implicit algorithm into the Eilmer3 CFD code
Responsibles: Dr. Pénélope Leyland, Ojas Joshi
Interdisciplinary Aerodynamics Group – IAG
Abstract
The work presented has the aim to implement the point-implicit scheme inside the Eilmer3
code. Once the scheme is integrated into the existing code, three different approaches can be
compared to different simulations. Two gas models are adopted in order to study the improvement
of the point-implicit scheme: the ideal gas model and the 11 species and 2-temperature gas model.
Performances of three different schemes are compared, once they are applied to these two di↵erent
gas models: the explicit scheme, the implicit scheme (which uses the point-implicit scheme in both
viscous and inviscid update), the hybrid scheme (which uses the point-implicit scheme only for
the viscous update). It turns out that the hybrid scheme has the best performances: the implicit
scheme has worse performances from the point of view of the simulation time, while the explicit
scheme has worse performance concerning the computation time, and the convergence is also
slower.
Fabien MARGAIRAZ – Particle-In-Cell and Particle-In-Fourier methods
Supervisors: Prof. Laurent Villard, Dr. Stephan Brunner, Dr. Sébastien Jolliet
Centre de Recherches en Physique des Plasmas – CRPP
Context
Turbulence in magnetized plasmas is known to induce heat, particle and momentum transport at levels typically much larger than that due to collisional processes alone. It leads to a degradation of the quality of confinement in magnetic fusion experiments.
First principles simulations of turbulence are based on a variety of numerical schemes. In particular, a Lagragian, Particle-In-Cell (PIC), Finite Element scheme is used in the ORB5/NEMORB suite of codes developed at CRPP in collaboration with the Max-Planck IPP in Garching.
Whereas the ORB5/NEMORB code has been shown to scale well up to 32k cores, bottle¬necks to further scalability have been identified, related to the way particles interact with the finite element grid used to solve for EM fields. This has prompted a reexamination of the algorithms used.
The intrisic problem of PIC schemes is the accumulation of statistical sampling noise. In ORB5/NEMORB the fields are Fourier transformed, then a filter is applied that eliminates unphysical modes, Fourier transformed back to real space. This has proven very efficient at reducing noise, however at the expense of communications. A source of the problem is that the real space 3D grid data size that needs to be communicated across processors far exceeds the Fourier space data size for physically meaningful modes. Hence the idea of going directly from particle data to physically meaningful Fourier space modes and dispensing with real space grid.
Brief Project Description
In this project, an alternative scheme, using projections on Fourier modes rather than projections on finite elements, is examined as a possible candidate to alleviate some of the scalability problems.
Instead of the 5D gyrokinetic turbulence problem in magnetic plasmas, a simpler phys¬ical model will be considered, namely the Vlasov-Poisson system describing electrostatic perturbations in a collisionless plasma, in a 2D phase space (x,v).
1) A code based on the standard PIC-delta-f finite element formulation will be written and tested.
2) This code will then be modified according to a new “Particle-In-Fourier” (PIF) scheme, i.e. replacing the particle-to-grid (and v.v.) operations with particle-to-Fourier-modes (and v.v.) ones.
3) Single process performance will be measured for both code versions (PIC and PIF) and for various problem sizes. Ways to optimize the PIF operations will be searched.
4) If time permits, the code will be parallelized with domain cloning and/or domain decomposition parallel schemes, using MPI and/or OpenMP. Parallel scalability tests will be then performed.
The codes will be developed in Fortran and make use of various libraries for Fourier transforms, finite elements and linear algebra.
Nicolò Pagan – Numerical Approximation of PDEs with Isogeometric Analysis and implementation in the LiveV library
Supervisor: Dr. Luca Dede’
Chair of Modelling and Scientific Computation – CMCS
Abstract
The aim of the project is double: to understand the flexibility of the Isogeometric Analysis tools through the solution of some PDEs problems; to test the improvement in the computational time given by a partial loops vectorization at compile-time of the LifeV IGA code. Three different applications have been selected: the potential flow problem around an airfoil profile, the heat equation problem in a bent cylinder and the Laplace problem in a multi-patches geometry representing a blood vessels bifurcation. The geometries used are built through the NURBS package available with the software GeoPDEs. The numerical analysis of the first application is performed with both GeoPDEs and LifeV IGA code. The comparison between different implementations shows that the degrees of freedom loop vectorization at compile-time is able to reduce the matrix assembling time of around 20%. The automatic vectorization at compile-time of the loop on the elements requires too much computational effort without having a reasonable improvement in the running time performances. Unsteady problems and multi-patches geometry have not been tested with LifeV IGA code, but GeoPDEs results show the expected solutions.
Jérémie Despraz – Indirect encodings for soft-multicellular robots
Professor: Dario Floreano
Assistants: Andrea Measani, Jürg Makus Germann
Laboratory of Intelligent Systems – LIS
Description
Since the seminal work of Sims on virtual creatures, different systems for the evolution of morphology and control of modular robots have been proposed. However, the aim of generating the morphology of a modular robot that could reach levels of complexity comparable to the ones observed in natural systems is far from being achieved.
To achieve this goal, many challenges must still be solved. It is clear that to design the structures of such multi-cellular robots, automatic design methods are needed that could possibly replicate the incredible diversity level produced by nature in an artificial system. Various generative encodings have been proposed in the past, including grammatical-encoding and methods that simulate natural morphogenesis.
In this project, the student will investigate existing indirect encodings for multi-cellular systems and test them on morphology matching problems. Furthermore, as test problem, he will investigate the emergence of skeletal structures in a soft-multi cellular robot. In the first part of the project, the student is expected to review existing encodings for the automatic design of multi-cellular structures. Then, the student will perform with the selected encodings a series of experiments to evaluate their capabilities on morphology matching benchmarks. Finally, he will employ the best encoding to evolve multi-cellular structures composed of cells having varying levels of stiffness to investigate the conditions that favours the evolution of skeletal structures.
Pascal Bienz – Artifact reduction in phase-contrast X-ray imaging
Supervision: Prof. Michael Unser and Masih Nilchian
Laboratory of Medical and Biological Images – LIB
Description
Grating interferometry is a phase-contrast X-ray imaging method that is extraordinarily sensitive to density variations in the sample. The method is especially suited for imaging of biomedical samples and will play an indispensable role in future X-ray imaging applications. However, the high sensitivity to variations in the sample is accompanied by a high sensitivity to intensity fluctuations (horizontal streaks) during image acquisition. The latter lead to artifacts in the 3D reconstructions, which in turn constitute a major obstacle for 3D data visualization and analysis.
The goal of the project is to design and test out image processing algorithms to reduce these artifacts. The potential impact of such work could be quite significant; in case of success, it would be immediately incorporated in the data processing pipeline of the TOMCAT beamline at the Swiss Light Source (Paul Scherrer Institute).
Hainan Hu – Analysis of thin film solar cells with OpenMax
Supervisors: Dr. Franz-Josef Haug and Mr. Ali Naqavi
Photovoltaics and thin film Electronics Laboratory PV-LAB
Abstract
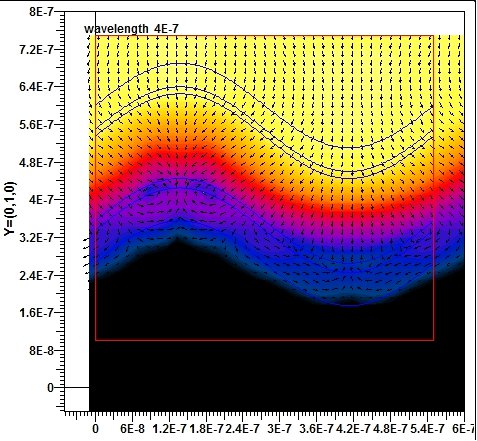
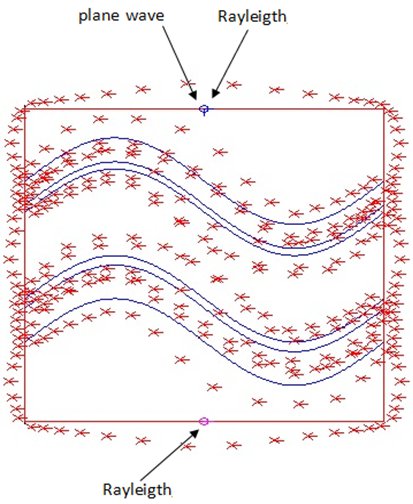
The Multiple Multipole Program(MMP) is developed ba Hafner in 1980. The first goal of this program is to obtain accurate and reliable solution of problems with computer. It’s a pure boundary method implementation, the field of each domain is evaluated by a series of expansions, which includs Multipole expansion, plane wave, Rayleigh expansion, Bessel expansion, etc. The basic function if this method fulfills Maxwell’s equations. This method belongs to groups of generalized multipole technique (GMT). This method can achieve a very high accuracy but the establishment of the model is very hard, because the allocation of multipolar function origins is not an easy job. In order to solve this problem, several trials to optimize the setting of multipole.
OpenMaX is a graphical electromagnetics platform with a number of electromagnetic solvers to solve the problem. It can also visualize the field solution, such as vector plots and animation to enhance understanding if the solution.
In this project, we had a quick theoretical study of the method (multiple-multipole) at start, then becoming familiar with the software and application to a simple problem: Sinusoidal grating structure thin film solar cell.
We compared our result with another method which widely used in the optical simulation of the solar cells : RCWA method, from the results we can see there are some parts of EQE curve of TE and TM simulations are quite different, we analysis the result of where possible differences comes from, the efficiency of these two methods and draw a possible future of the work.
Dana Christen – Development of QMMM/MD software for biomolecular modeling
Professor: Matteo Dal Peraro
Laboratory for Biomolecular Modeling – LBM
Description
While providing the most accurate results, quantum molecular dynamics simulations are limited to small systems due to the very high computation times they require. Classical molecular dynamics on the other hand allows larger simulations at the expense of less accurate results.
Hybrid simulations aim at modeling large molecular systems using conventional classical methods while involving quantum mechanics algorithms to enhance subsets of the simulation domain, thus combining reasonable computation time and accurate results in critical areas.
The goal of this project is to implement a basic hybrid framework inside of the molecular simulation software NAMD.
Fabrizio Rompineve Sorbello – Aspects of hard scatterings in current LHC analysis
Supervisor: Prof. Stefano Frixione
Institute of Theoretical Physics – ITP & CERN
Abstract
The primary aim of this project is that of exploiting a set of computer codes, collectively known as aMC@NLO (see amcatnlo.cern.ch), that are able to compute, numerically and in a fully automated manner, the cross sections for any user-defined scattering processes at the first non-trivial order in the perturbation theory of the coupling constant of QCD (the theory of strong interactions, which is dominant at the LHC). Such cross sections may or may not be combined with an Event Generator simulation, which allows one to obtain final states that are faithful representations of those actually occurring in high-energy hadron collisions.
The idea is that of investigating aspects of hard scatterings that pose challenging problems in current LHC analyses. These include the production of a Standard-Model Higgs boson in association with up to two light jets, and with a top-antitop pair, and that of a W boson is association with light jets. The achievement of this project requires a command of the aMC@NLO codes, the ability to understand the physics of an Event Generator, and the capability to write a physics analysis to be employed in the latter. Although most of the aMC@NLO codes are set up and tested, parts of this project could require the writing of code add-ons.
Cyril Misev – Single Particle Simulation in 3D Tokamak magnetic fields
Responsibles: Dr. Jonathan Graves, David Pfefferlé
Centre de Recherches en Physique des Plasmas – CRPP
Abstract
The objective of this project is to contribute to the improvement of an existing code used for simulating the behaviour of a population of particles in a magnetic field. Improvements will take into account calculation speed and accuracy (physical and numerical).
The guiding centre particle trajectory code to be improved presently employs tri-linear interpolation of the 3D magnetic field in order to propagate the trajectory equations for the single particle position as it moves through the magnetic field. This can cause error, especially where the grid is coarse relative to the variation in the magnetic field.
The external magnetic field contributions are provided from an equilibrium code through Fourier modes in the poloidal and toroidal directions, but discretized in the third (radial) direction. However in the guiding centre code, the toroidal and poloidal coordinates are presently discretised and interpolated. The goal is in part to avoid this unnecessary discretisation step in the poloidal and toroidal coordinates, and thus to calculate the set of magnetic field values at the exact position of the particle at every timestep of the simulation.
To further reduce computation time, the code should find an optimum minimum number of toroidal and poloidal modes yielding a prescribed acceptable error in the equilibrium from the equilibrium code. A special requirement to the code is that physical properties, most importantly div(B)=0 must be satisfied. Regarding the discretisation in the radial direction, the goal will be to implement a variable (non-equidistant) grid.
Convergence studies of trajectories as well as simulation time comparisons with the initial code will be done using different interpolation techniques and radial grid point distributions will be used to test the new code in terms of its efficiency.
Duccio Malinverni – Dynamical Monte-Carlo simulation of polymers in confined space: Implementation of a new algorithm
Responsible: Prof. Pablo De Los Rios
Laboratory of Statistical Biophysics – LBS
Description
Polymers confined in space are present in many real-life applications: Compacted DNA, thin layers, physics of dielectrics among others. The conformation of such polymers leads to a competition between imposed external geometry and internal arrangement of the monomers composing the polymer. The complexity of these arrangement naturally lead to the use of computer simulations of these systems in the field of statistical physics of polymers. Among the family of Monte-Carlo simulations, two types of algorithms exist:
The statical approach consists of sequentially adding a monomer to the polymer chain in a random direction, rejecting the chains which violate compatibility with the general chain (no monomer overlap, chain inside the geometry domain) until a given number of polymers of N monomers are generated.
The dynamical method starts with a chain of N monomers, and stochastically moves a randomly chosen monomer in a random direction, then again checking if the new conformation is compatible with the internal and external constraints until a given number of polymer conformations are generated.
As the number of monomers is increased, and the confined space decreased, the dynamical method tends to reject more and more conformations mainly due to a conflict with the confined geometry.
In this project, a new dynamical algorithm is implemented in which the number of these rejections should be decreased while generating conformations. The goal of this project is to implement this algorithm, validate it against theoretical (end-to-end distance and gyration radius, auto-correlation function,…) and other numerical methods, and benchmark its performance.
Dana Christen – Multi-level preconditioner for solving the Navier-Stokes equations in hemodynamics applications
Responsibles: Dr. Simone Deparis, Mr. Gwenol Grandperrin
Chair of Modelling and Scientific Computing – CMCS
Description
We present a multi-level algorithm to approximate the inverse of the fluid block in a Navier-Stokes saddle-point matrix where the coarse level is defined as a restriction of the degrees of freedom to the degrees of a lower order finite elements approximation.
A one-level scheme involving P1 and P2 finite elements is studied in details and several transfer operators are compared by means of two reference problems.
Numerical results show that restriction and prolongation operators based on projection techniques lead to faster GMRES convergence of the fluid part, when compared to operators based on interpolation techniques.
Federico Hernan Martinez Lopez – Solving didactical problems with CUDA
Supervisors: Prof. Roger Hersch and Remi Bloch
Peripheral Systems Laboratory – LSP
Description
The objective of the project is to implement some algorithms which by nature expose high parallelization and some others that may not be so obvious in the GPGPU. The main tasks will be:
– Identification of massively parallel regions of the algorithms
– Implementation of the algorithms in GPGPU
– Identification and implementation of performance improvement in running time
– Analysis of the theoretical vs practical speedup
– Comparison of results with different parallel architectures (Multicore, clusters, etc)
Ivan Slijepcevic – A Parallel Particle Swarm Optimization engine for a universal optimization environment
Supervisor: Prof. Matteo Dal Peraro
Laboratory for Biomolecular Modeling – LBM
Description
In some optimization problems the evaluation of the fitness function may require complex operations, that cannot be represented by a simple algebraic expression. These operations may typically involve manipulations of files or complex data structures, as well as calls to an external programs.
Parallel Optimization Workbench (POW) is a python-based optimization framework helping the developer to tackle these problems with minimal production of code. In order to evaluate the fitness function, POW allows the manipulation of any data structure as well as the call of external programs. The exploration of the search space is performed by an enhanced version of Particle Swarm Optimization (PSO Kick and Reseed, PSO-KaR), working in a parallel fashion using MPI libraries.
The aim of this project is to implement PSO-KaR in C++ and integrate it in the existing POW framework. The code will be benchmarked against the original Python implementation on multicore workstations first, and finally on a cluster.
Lidia Stepanova – Reduced order models for the simulation of pathological heart valves
Supervisor: Dr. Simone Deparis and Dr. Toni Lassila
Chair of Modelling and Scientific Computing – CMCS
Description
The human heart contains four biological valves (mitral, aortic, pulmonary, and tricuspid) that regulate the flow in the atria and the ventricles. Malfunction of one of these valves, either by stenosis (stiffening resulting in a inability to open properly) or by regurgitation (leakage or flow reversal due to an inability to close properly), is a relatively common condition affecting the function of the heart and potentially leading to the onset of heart failure. There is much interest in the modelling and simulation of heart valves. especially pathological ones, in order to predict and prescribe possible surgical therapies in patient-specific cases. In the case that insufficient data and/or modelling capability is available to fully capture the complex 3D interaction between the valves and the blood flow through the heart, we want to capture the general behavior of the valve in the sense of mean flow, intraventricular pressure, and other clinically relevant variables. To this end many works have been devoted to deriving lumped parameter models for heart valves. They do not model the entire 3D geometry and fluid-structure interaction of the valve, but rather work based on simplified fluid dynamics principles and integrated quantities of velocity and pressure across the valve surface. The objectives of this project are to first perform an overview of existing reduced order models for the heart valves, and then to choose a suitable subset of models to prototype in MatLab and further to implement in LifeV library. Comparisons between predictions given by different reduced models for valves should be made first between artificial test cases, and finally on real patient data obtained as part of a project related to the simulation of pathological left ventricles with regurgitant mitral valves.
Laurent Fasnacht – Verifying equivalence of Python programs to their C/C++ counterparts
Supervisor: Prof. George Candea
Dependable Systems Laboratory – DSLAB
Abstract
When developing HPC software, it is common to first write a prototype in a high level language (MATLAB, Python, R, …), to ensure the correctness of the algorithm and have a first usable implementation. However, these programming languages, while allowing quick code writing, don’t allow the same performance as low-level languages, like C or C++. Therefore, developers usually reimplement the algorithms in a more efficient language, and then make some checks to give themselves some confidence that both implementations give the same results. As writing good tests is difficult, it would be very useful to have tools that are able to prove equivalence between both implementations (check that for all possible inputs, outputs are equivalent).
This project focuses on proving equivalence between programs in Python and C. The main idea is to write a tool chain based on selected existing tools to convert both languages to a common representation, on which it becomes possible to apply automated reasoning techniques to formally prove equivalence. As the result of the proof depends on the quality of the tools doing the conversion, they have to be checked in depth. The tool chain will then be integrated in a framework that enables developers to easily verify their code.
Andrea Di Blasio – Numerical simulation of blood solutes by Isogeometric Analysis
Supervisor: Dr. Luca Dede’
Chair de Modelling and Scientific Computing – CMCS
Description
Solutes and drugs are transported in the circulatory system by the blood for which absorption processes occur at the arterial walls. The comprehension, modeling, and simulation of these phenomena, both in physiological and pathological conditions, represents a relevant topic of interest in biomedical applications. Different mathematical models can be considered by coupling the Navier-Stokes equations representing the blood flow with the advection-diffusion equations describing the transport of the solutes and eventually the diffusion processes in the arterial wall, thus defining heterogeneous coupled models.
The project focus on the numerical approximation by means of Isogeometric Analysis of the Navier-Stokes equations coupled with the advection-diffusion models for the dynamics of the solutes in the blood and in the arterial walls. Firstly, the case of steady problems should be considered. Then, unsteady problems could be solved by using suitable numerical scheme for the approximation in time of the coupled problem. In both the cases, two-dimensional problems can be studied.
Elena Queirolo – Numerical methods for trajectory optimisation
Supervisor: Prof. Assyr Abdulle and Martin Huber
Chaire d’analyse numérique et mathématiques computationnelles – ANMC
Description
The optimal design of the trajectory of a spacecraft is an important problem in aeronautics. For example, the task could be to find the best trajectory when the destination and the maximal fuel consumption are given. The aim of the project is to study a numerical method for such trajectory optimization modeled as an optimal control problem. First, we derive the first order optimality conditions of the optimal control problem and reformulate them as a constrained Hamiltonian system with two-point boundary conditions. Then, we use symplectic partitioned Runge-Kutta methods for the discretization in time and analyze their properties. Finally, we obtain the numerical method by combining these Runge-Kutta methods with a multiple shooting algorithm. We illustrate the capabilities of the numerical method by solving a model problem.
Loïc Perruchoud – Tracking leg movements in high-speed videos of insect locomotion
Biomedical Imaging Group – BIG
Supervisors: Prof. Michael Unser, Dr. Cédric Vonesch, Pavan Ramdya
Description
In order to study locomotion in Drosophila, one must be able to quantify with high precision their walking behaviours. Therefore, the goal of this project is to build a computer vision software that extracts information on the positions and orientations of various leg segments from video input of Drosophila in an automated way. This work was separated into two major parts.
The first part reported the tracking of the body of a fly. This task was completed using an active snake. We first introduce the basics of active snakes and presented how the evolution of the curve define by the snake can be formulated as an optimization problem. Then, we introduced various fly models that we used. We finally showed how it is possible to track the body of a fly using active snake with a shape regularization energy term. The tracking algorithm showed good performances and robustness.
In the second part, we have been able to extend the optimization procedure used to track the body to the legs. We defined a parametric model of legs that can be attached to the body as a function of the active snake tracking the body. The tracking problem was formulated as an optimization problem thanks to an energy term based on the response of the fly to a steerable ridge filter. We showed that by adding two geometric constraint energy terms, we were able to obtain promising results for the tracking of the legs of the fly.
Fabrizio Rompineve Sorbello – Aspects of hard scatterings in current LHC analysis
Supervisor: Prof. Stefano Frixione
Institute of Theoretical Physics – ITP & CERN
Abstract
The primary aim of this project is that of exploiting a set of computer codes, collectively known as aMC@NLO (see amcatnlo.cern.ch), that are able to compute, numerically and in a fully automated manner, the cross sections for any user-defined scattering processes at the first non-trivial order in the perturbation theory of the coupling constant of QCD (the theory of strong interactions, which is dominant at the LHC). Such cross sections may or may not be combined with an Event Generator simulation, which allows one to obtain final states that are faithful representations of those actually occurring in high-energy hadron collisions.
The idea is that of investigating aspects of hard scatterings that pose challenging problems in current LHC analyses. These include the production of a Standard-Model Higgs boson in association with up to two light jets, and with a top-antitop pair, and that of a W boson is association with light jets. The achievement of this project requires a command of the aMC@NLO codes, the ability to understand the physics of an Event Generator, and the capability to write a physics analysis to be employed in the latter. Although most of the aMC@NLO codes are set up and tested, parts of this project could require the writing of code add-ons.
Cyril Misev – Single Particle Simulation in 3D Tokamak magnetic fields
Responsibles: Dr. Jonathan Graves, David Pfefferlé
Centre de Recherches en Physique des Plasmas – CRPP
Abstract
The objective of this project is to contribute to the improvement of an existing code used for simulating the behaviour of a population of particles in a magnetic field. Improvements will take into account calculation speed and accuracy (physical and numerical).
The guiding centre particle trajectory code to be improved presently employs tri-linear interpolation of the 3D magnetic field in order to propagate the trajectory equations for the single particle position as it moves through the magnetic field. This can cause error, especially where the grid is coarse relative to the variation in the magnetic field.
The external magnetic field contributions are provided from an equilibrium code through Fourier modes in the poloidal and toroidal directions, but discretized in the third (radial) direction. However in the guiding centre code, the toroidal and poloidal coordinates are presently discretised and interpolated. The goal is in part to avoid this unnecessary discretisation step in the poloidal and toroidal coordinates, and thus to calculate the set of magnetic field values at the exact position of the particle at every timestep of the simulation.
To further reduce computation time, the code should find an optimum minimum number of toroidal and poloidal modes yielding a prescribed acceptable error in the equilibrium from the equilibrium code. A special requirement to the code is that physical properties, most importantly div(B)=0 must be satisfied. Regarding the discretisation in the radial direction, the goal will be to implement a variable (non-equidistant) grid.
Convergence studies of trajectories as well as simulation time comparisons with the initial code will be done using different interpolation techniques and radial grid point distributions will be used to test the new code in terms of its efficiency.
Duccio Malinverni – Dynamical Monte-Carlo simulation of polymers in confined space: Implementation of a new algorithm
Responsible: Prof. Pablo De Los Rios
Laboratory of Statistical Biophysics – LBS
Description
Polymers confined in space are present in many real-life applications: Compacted DNA, thin layers, physics of dielectrics among others. The conformation of such polymers leads to a competition between imposed external geometry and internal arrangement of the monomers composing the polymer. The complexity of these arrangement naturally lead to the use of computer simulations of these systems in the field of statistical physics of polymers. Among the family of Monte-Carlo simulations, two types of algorithms exist:
The statical approach consists of sequentially adding a monomer to the polymer chain in a random direction, rejecting the chains which violate compatibility with the general chain (no monomer overlap, chain inside the geometry domain) until a given number of polymers of N monomers are generated.
The dynamical method starts with a chain of N monomers, and stochastically moves a randomly chosen monomer in a random direction, then again checking if the new conformation is compatible with the internal and external constraints until a given number of polymer conformations are generated.
As the number of monomers is increased, and the confined space decreased, the dynamical method tends to reject more and more conformations mainly due to a conflict with the confined geometry.
In this project, a new dynamical algorithm is implemented in which the number of these rejections should be decreased while generating conformations. The goal of this project is to implement this algorithm, validate it against theoretical (end-to-end distance and gyration radius, auto-correlation function,…) and other numerical methods, and benchmark its performance.
Dana Christen – Multi-level preconditioner for solving the Navier-Stokes equations in hemodynamics applications
Responsibles: Dr. Simone Deparis, Mr. Gwenol Grandperrin
Chair of Modelling and Scientific Computing – CMCS
Description
We present a multi-level algorithm to approximate the inverse of the fluid block in a Navier-Stokes saddle-point matrix where the coarse level is defined as a restriction of the degrees of freedom to the degrees of a lower order finite elements approximation.
A one-level scheme involving P1 and P2 finite elements is studied in details and several transfer operators are compared by means of two reference problems.
Numerical results show that restriction and prolongation operators based on projection techniques lead to faster GMRES convergence of the fluid part, when compared to operators based on interpolation techniques.
Federico Hernan Martinez Lopez – Solving didactical problems with CUDA
Supervisors: Prof. Roger Hersch and Remi Bloch
Peripheral Systems Laboratory – LSP
Description
The objective of the project is to implement some algorithms which by nature expose high parallelization and some others that may not be so obvious in the GPGPU. The main tasks will be:
– Identification of massively parallel regions of the algorithms
– Implementation of the algorithms in GPGPU
– Identification and implementation of performance improvement in running time
– Analysis of the theoretical vs practical speedup
– Comparison of results with different parallel architectures (Multicore, clusters, etc)
Ivan Slijepcevic – A Parallel Particle Swarm Optimization engine for a universal optimization environment
Supervisor: Prof. Matteo Dal Peraro
Laboratory for Biomolecular Modeling – LBM
Description
In some optimization problems the evaluation of the fitness function may require complex operations, that cannot be represented by a simple algebraic expression. These operations may typically involve manipulations of files or complex data structures, as well as calls to an external programs.
Parallel Optimization Workbench (POW) is a python-based optimization framework helping the developer to tackle these problems with minimal production of code. In order to evaluate the fitness function, POW allows the manipulation of any data structure as well as the call of external programs. The exploration of the search space is performed by an enhanced version of Particle Swarm Optimization (PSO Kick and Reseed, PSO-KaR), working in a parallel fashion using MPI libraries.
The aim of this project is to implement PSO-KaR in C++ and integrate it in the existing POW framework. The code will be benchmarked against the original Python implementation on multicore workstations first, and finally on a cluster.
Lidia Stepanova – Reduced order models for the simulation of pathological heart valves
Supervisor: Dr. Simone Deparis and Dr. Toni Lassila
Chair of Modelling and Scientific Computing – CMCS
Description
The human heart contains four biological valves (mitral, aortic, pulmonary, and tricuspid) that regulate the flow in the atria and the ventricles. Malfunction of one of these valves, either by stenosis (stiffening resulting in a inability to open properly) or by regurgitation (leakage or flow reversal due to an inability to close properly), is a relatively common condition affecting the function of the heart and potentially leading to the onset of heart failure. There is much interest in the modelling and simulation of heart valves. especially pathological ones, in order to predict and prescribe possible surgical therapies in patient-specific cases. In the case that insufficient data and/or modelling capability is available to fully capture the complex 3D interaction between the valves and the blood flow through the heart, we want to capture the general behavior of the valve in the sense of mean flow, intraventricular pressure, and other clinically relevant variables. To this end many works have been devoted to deriving lumped parameter models for heart valves. They do not model the entire 3D geometry and fluid-structure interaction of the valve, but rather work based on simplified fluid dynamics principles and integrated quantities of velocity and pressure across the valve surface. The objectives of this project are to first perform an overview of existing reduced order models for the heart valves, and then to choose a suitable subset of models to prototype in MatLab and further to implement in LifeV library. Comparisons between predictions given by different reduced models for valves should be made first between artificial test cases, and finally on real patient data obtained as part of a project related to the simulation of pathological left ventricles with regurgitant mitral valves.
Laurent Fasnacht – Verifying equivalence of Python programs to their C/C++ counterparts
Supervisor: Prof. George Candea
Dependable Systems Laboratory – DSLAB
Abstract
When developing HPC software, it is common to first write a prototype in a high level language (MATLAB, Python, R, …), to ensure the correctness of the algorithm and have a first usable implementation. However, these programming languages, while allowing quick code writing, don’t allow the same performance as low-level languages, like C or C++. Therefore, developers usually reimplement the algorithms in a more efficient language, and then make some checks to give themselves some confidence that both implementations give the same results. As writing good tests is difficult, it would be very useful to have tools that are able to prove equivalence between both implementations (check that for all possible inputs, outputs are equivalent).
This project focuses on proving equivalence between programs in Python and C. The main idea is to write a tool chain based on selected existing tools to convert both languages to a common representation, on which it becomes possible to apply automated reasoning techniques to formally prove equivalence. As the result of the proof depends on the quality of the tools doing the conversion, they have to be checked in depth. The tool chain will then be integrated in a framework that enables developers to easily verify their code.
Andrea Di Blasio – Numerical simulation of blood solutes by Isogeometric Analysis
Supervisor: Dr. Luca Dede’
Chair de Modelling and Scientific Computing – CMCS
Description
Solutes and drugs are transported in the circulatory system by the blood for which absorption processes occur at the arterial walls. The comprehension, modeling, and simulation of these phenomena, both in physiological and pathological conditions, represents a relevant topic of interest in biomedical applications. Different mathematical models can be considered by coupling the Navier-Stokes equations representing the blood flow with the advection-diffusion equations describing the transport of the solutes and eventually the diffusion processes in the arterial wall, thus defining heterogeneous coupled models.
The project focus on the numerical approximation by means of Isogeometric Analysis of the Navier-Stokes equations coupled with the advection-diffusion models for the dynamics of the solutes in the blood and in the arterial walls. Firstly, the case of steady problems should be considered. Then, unsteady problems could be solved by using suitable numerical scheme for the approximation in time of the coupled problem. In both the cases, two-dimensional problems can be studied.
Elena Queirolo – Numerical methods for trajectory optimisation
Supervisor: Prof. Assyr Abdulle and Martin Huber
Chaire d’analyse numérique et mathématiques computationnelles – ANMC
Description
The optimal design of the trajectory of a spacecraft is an important problem in aeronautics. For example, the task could be to find the best trajectory when the destination and the maximal fuel consumption are given. The aim of the project is to study a numerical method for such trajectory optimization modeled as an optimal control problem. First, we derive the first order optimality conditions of the optimal control problem and reformulate them as a constrained Hamiltonian system with two-point boundary conditions. Then, we use symplectic partitioned Runge-Kutta methods for the discretization in time and analyze their properties. Finally, we obtain the numerical method by combining these Runge-Kutta methods with a multiple shooting algorithm. We illustrate the capabilities of the numerical method by solving a model problem.
Loïc Perruchoud – Tracking leg movements in high-speed videos of insect locomotion
Biomedical Imaging Group – BIG
Supervisors: Prof. Michael Unser, Dr. Cédric Vonesch, Pavan Ramdya
Description
In order to study locomotion in Drosophila, one must be able to quantify with high precision their walking behaviours. Therefore, the goal of this project is to build a computer vision software that extracts information on the positions and orientations of various leg segments from video input of Drosophila in an automated way. This work was separated into two major parts.
The first part reported the tracking of the body of a fly. This task was completed using an active snake. We first introduce the basics of active snakes and presented how the evolution of the curve define by the snake can be formulated as an optimization problem. Then, we introduced various fly models that we used. We finally showed how it is possible to track the body of a fly using active snake with a shape regularization energy term. The tracking algorithm showed good performances and robustness.
In the second part, we have been able to extend the optimization procedure used to track the body to the legs. We defined a parametric model of legs that can be attached to the body as a function of the active snake tracking the body. The tracking problem was formulated as an optimization problem thanks to an energy term based on the response of the fly to a steerable ridge filter. We showed that by adding two geometric constraint energy terms, we were able to obtain promising results for the tracking of the legs of the fly.